東大寺2015年度算数 大問3⑴

「東大寺算数を解いてみた」シリーズ。
今回の問題は、円2個が大きな円の周囲を転がるという、あまり見慣れない（？）問題。

【図1】のようなA，B，Cを中心とする，小，中，大3つの円板(ア)，(イ)，(ウ)があります。(ア)，(イ)の半径はそれぞれ2cm，3cmです。また，P，Q，Rはそれぞれの周上の点です。これらを【図2】のように，3点P，Q，Rがすべて重なるようにおき，(ア)は(ウ)の内側を，(イ)は(ウ)の外側を，離れることもすべることもなく，それぞれ【図2】の矢印の向きに回転させながら，(ウ)の周に沿ってちょうど一周だけ動かします。ただし，3つの中心C，A，Bが常に1つの直線上に並ぶように動かすものとします。

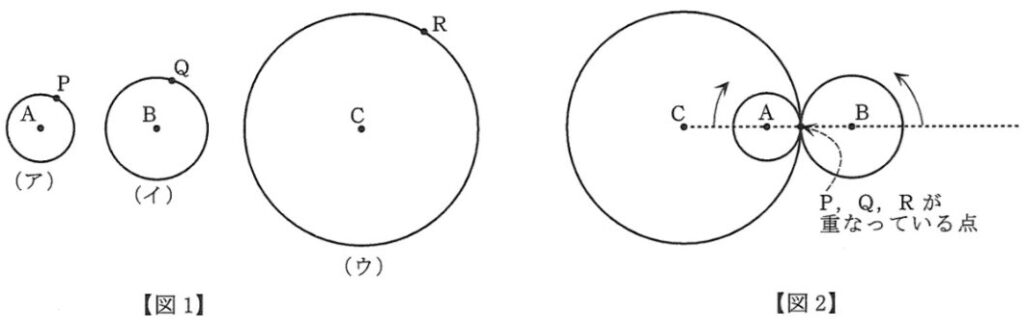
【図3】のように3点C，A，Bを通る直線と2点C，Rを通る直線とでできる角が30°になるまで(ア)，(イ)を動かしたとき，APとBQが平行になりました。

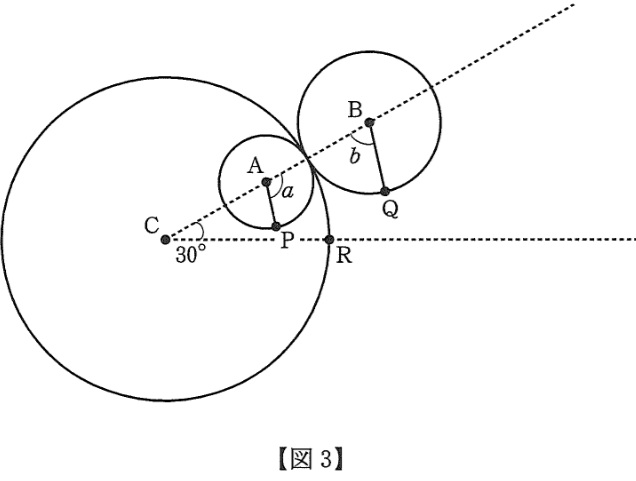
①　【図3】の角aと角bの大きさの比を最も簡単な整数の比で答えなさい。
②　円板(ウ)の半径を求めなさい。

次の図を参考にして、読み進めてください。

上の図で弧DP＝弧DR＝弧DQになっているはずです。
①では、弧DP＝弧DQを使いましょう。
弧DP＝2×2×π×\(\frac{a}{360}\)＝\(\frac{a}{90}\)×π
弧DQ＝3×2×π×\(\frac{b}{360}\)＝\(\frac{b}{60}\)×π
\(\frac{a}{90}\)×π＝\(\frac{b}{60}\)×πなので、
\(\frac{a}{90}\)＝\(\frac{b}{60}\)
つまり、a×\(\frac{1}{90}\)＝b×\(\frac{1}{60}\)となるので、
a：b＝3：2です。

②　弧DP＝弧DR　を使いましょう。
①からa：b＝3：2ですが、APとBQが平行なので、a＋b＝180度です。
ですから、a＝108度と分かります。
円Cの半径を□とすると、
弧DR＝□×2××π×\(\frac{30}{360}\)＝□×\(\frac{1}{6}\)×π
弧DP＝2×2×π×\(\frac{108}{360}\)＝1.2×π
よって、□×\(\frac{1}{6}\)＝1.2より、□＝7.2cm

以下は究学からのおすすめです。

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。