東大寺2024年度算数 大問2

「東大寺の算数を解いてみた」シリーズ。
2024年度の分に挑戦中です。
次は大問2の平面図形っぽい問題。

下の図のような五角形ABCDEがあります。角C，角D，角Eはすべて直角で，辺BC，辺DEの長さはそれぞれ10.5cm，33cmです。ACとBDの交点をFとするとき，三角形BCF，三角形AFDの面積はそれぞれ27cm²，432cm²です。このとき次の問いに答えなさい。

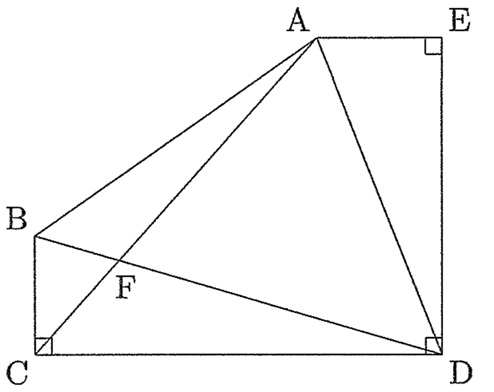
⑴　辺CDの長さを求めなさい。

まずは分かっていることを図に記入しないとね。
・辺BC，辺DEの長さはそれぞれ10.5cm，33cm
・三角形BCF，三角形AFDの面積はそれぞれ27cm²，432cm²
ここからすぐに分かることも記入するといい。

面積が分かっている2つの三角形にそれぞれ三角形FCD（★）を付け加えて考える。（付け足し「差」の考え方）
☆　同じものを付け足しても「差」は変わらない!!!

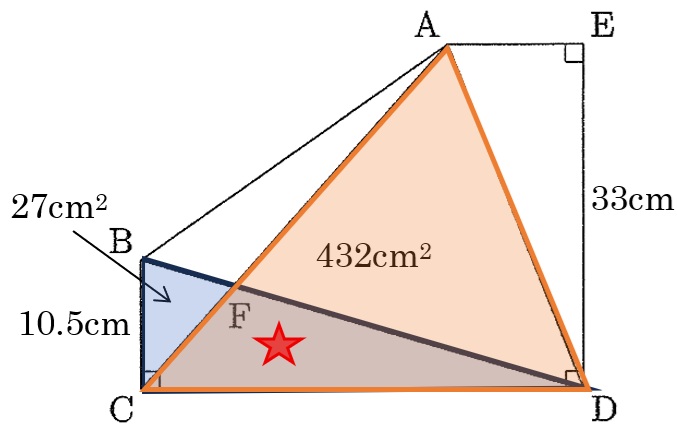
三角形AFD＋三角形FCD＝三角形ACD　→　CD×33÷2
三角形BCF＋三角形FCD＝三角形BCD　→　CD×10.5÷2
⇒　三角形ACD－三角形BCD＝CD×33÷2－CD×10.5÷2＝(33－10.5)×CD÷2
　また、三角形ACD－三角形BCDは、三角形AFD－三角形BCF＝432－27＝405cm²
なので、(33－10.5)×CD÷2＝405
ここからCDを求めよう。
CD＝405×2÷22.5＝36cmとなった。

⑵　三角形ADEの面積を求めなさい。

CD＝36cmと分かったので、三角形BCD＝10.5×36÷2＝189cm²より、三角形FCD＝189－27＝162cm²
三角形BCF：三角形FCD＝BF：FDで、BF：FD＝27：162＝1：6

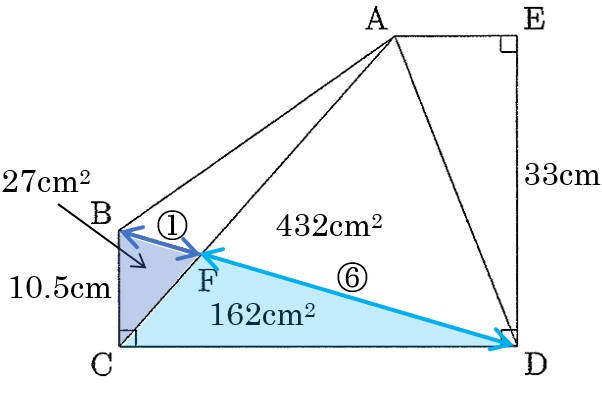
三角形ABF：三角形AFD＝1：6なので、三角形ABF＝432÷6＝72cm²
着々と正解に近づいてきた気がする・・・
底辺をBC(＝10.5cm)としたときの、三角形ABCとの高さと36cmの差がAEの長さになる！
三角形ABCの高さは(27＋72)×2÷10.5＝18\(\frac{6}{7}\)cm
AE＝36－18\(\frac{6}{7}\)＝17\(\frac{1}{7}\)cm
よって三角形ADEの面積は、17\(\frac{1}{7}\)×33÷2＝282\(\frac{6}{7}\)cm²となる。

究学からのご案内

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。

➪2024年度大阪星光算数入試問題と解説、見本を無料進呈しています。