「東大寺の算数を解いてみた」シリーズ。
2014年度大問5の立体図形の問題です。
けっこう難度が高い問題ですから、心してかかりましょう。ただし、取れる問題もあるので、それは絶対逃しちゃだめですよ。
右の図のようなAB=2cm,AD=3cm,AE=4cmの直方体ABCD-EFGHがあります。このとき,次の問いに答えなさい。
⑴ 点QがCH上を自由に動くとき,AQをAR:RQ=2:1に分ける点Rが動くことができる部分の長さは,CHの何倍ですか。
図のように、AR:RQは常に2:1なので、点QがCH上を動いていくと、それに平行に点Rも移動していきます。
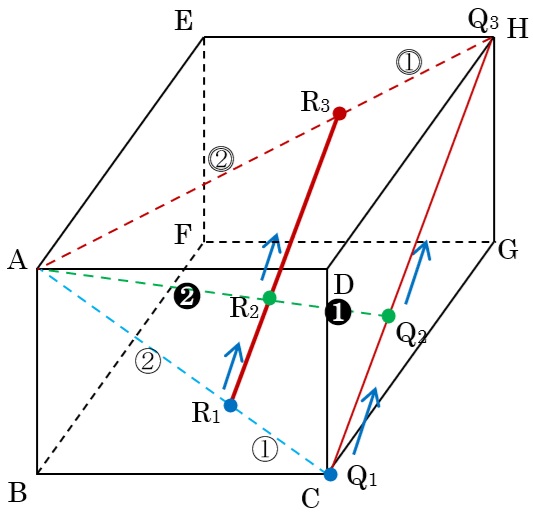
このとき、三角形ACHと図の三角形AR1R3は相似で、相似比は2:3なので、R1R3:CH=2:3
となるので、点Rが動くことができる部分の長さは,CHの\(\frac{2}{3}\)倍となります。
⑵ 点PはAF上を自由に動き,点Qは点Pの動きと無関係にCH上を自由に動きます。PQをPR:RQ=2:1に分ける点をRとするとき,点Rが動くことのできる範囲は,どのような図形になりますか。最も適切な名称で答えなさい。また,その図形の面積を求めなさい。
これはなかなか厳しい問題です。
見取り図に、先に挙げたような図を描いて考えようとしても、正確なところがさっぱりわからないのではないでしょうか。
ですが、まずは作業してみます。
ポイントは一方の点を止めて考えること。
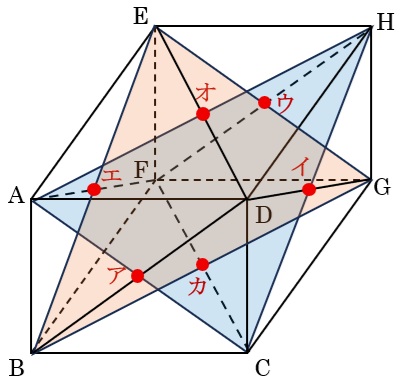
ア:PをAに固定し、Qだけ動かせばRは図のR1R2上を動きます。
イ:PをFに固定し、Qだけ動かせばRは図のR3R4上を動きます。
ウ:QをCに固定し、Pだけ動かせばRは図のR1R3上を動きます。
エ:QをHに固定し、Pだけ動かせばRは図のR2R4上を動きます。
ですから、点Rは図の色をつけた四角形R1R2R4R3の周囲とその内部を動くことができるはずです。
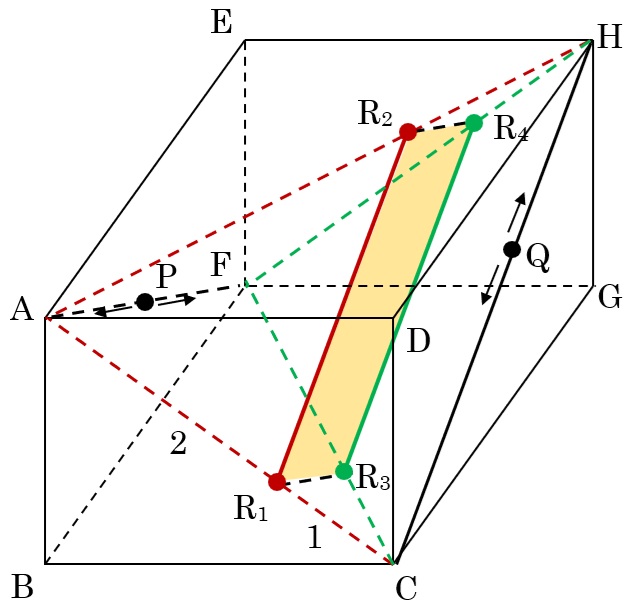
ところがここで大問題!!
この四角形は向かい合った辺が平行であることは分かりますが、果たしてそれは「平行四辺形」なのか「長方形」なのか、この段階ではさっぱり分かりません。
そこで、2:1に注目します。
Rは常にPQを2:1に分ける点なので、この図形を真上から見たとき、Rの存在できる場所がはっきりします。
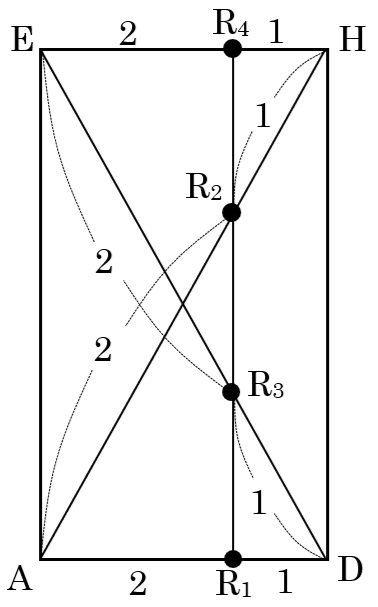
上の図から、Rは直方体の2つの向かい合った面ABFEとDCGHからの距離が2:1になる長方形の面上にある(もちろん、面ABFEともDCGHとも平行な面)ことが分かります。
そこで、面DCGH側からこの立体を見て、求めたい図形の形状と面積を求めましょう。

R1,R2,R3,R4をふくむ面で切断した面はたて2cm,横4cmの長方形で、色をつけた部分の形状は平行四辺形。
面積は長方形から4つの三角形を引いて求めます。
2×4-4×\(\frac{2}{3}\)×2×\(\frac{2}{3}\)÷2×2-4×\(\frac{1}{3}\)×2×\(\frac{1}{3}\)÷2×2=\(\frac{32}{9}\)cm2
⑶① 三角すいACFHの体積を求めなさい。ただし,三角すいの体積は(底面積)×(高さ)÷3で求めることができます。
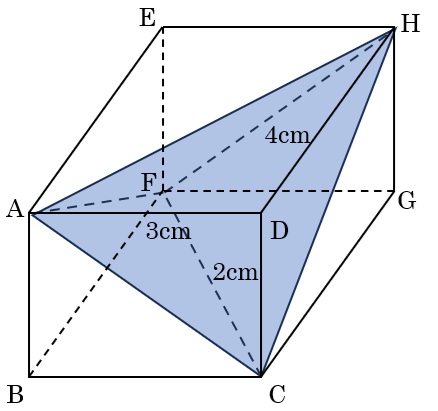
図の三角すいで、体積は2×3÷2×4÷3=4cm3
② 三角すいACFHと三角すいBDEGの共通部分(どちらの三角すいにも含まれている部分)の体積を求めなさい。
図を描いて考えますが、注目するのは「交点」です。
この2つの三角すいの辺が、もとの直方体の6つの面上で交わります。
この6つの点をつないでできる立体が、2つの三角すいの共通部分になります。
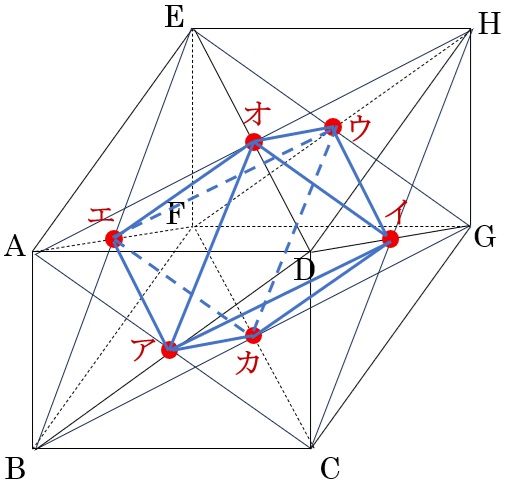
この立体は、底面を面アイウエとし,高さをオカとする八面体となります。
面アイウエの面積は長方形ADHEの半分なので、3×4÷2=6cm2、高さオカはABと同じで2cm
よって体積は、6×2÷3=4cm3です。
そして問題はまだ続きます。いい加減にしてほしい、と思ってしまいましたが…
⑷ ⑵で求めた図形のうち⑶の②の立体に含まれている部分の面積を求めなさい。
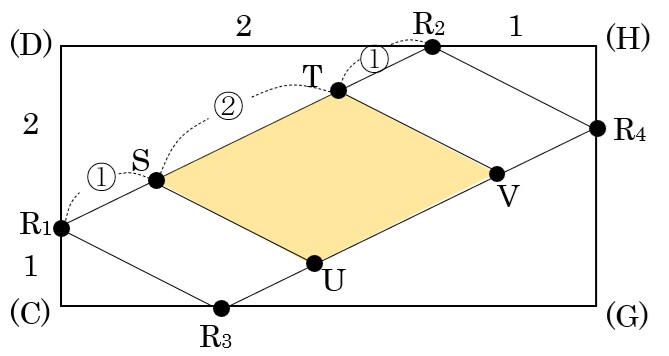
三角形ACHと三角形アイオは同じ面にある。
これに⑵のR1R2をかいて交点S,Tを求めてみよう。
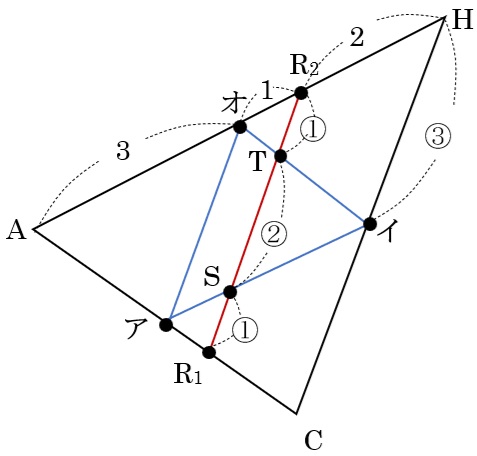
R1S:ST:TR2=1:2:1となる。
同様にR3R4も2点U,VでR3U:UV:VR4=1:2:1となる。
だから、求める面積は四角形STVUになり、これは⑵の面積の\(\frac{2}{1+2+1}\)=\(\frac{1}{2}\)なので、\(\frac{32}{9}\)×\(\frac{1}{2}\)=\(\frac{16}{9}\)cm2(次の図も参照。)
究学からのご案内
大阪星光を目指すなら
大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。
➪2024年度大阪星光算数入試問題と解説、見本を無料進呈しています。
オンライン個別指導で算数・国語も実力伸長!
算国オンライン個別指導塾究学の生徒も募集しています(年中いつでも歓迎します。まずは無料体験で)



