円が三角形に接しながら内部を通過~東大寺2020年度大問3⑴
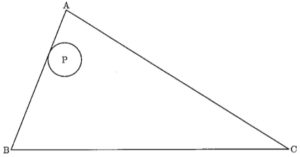
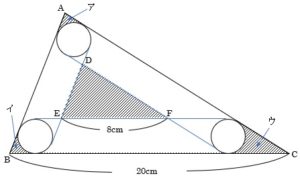
① 円Pを三角形ABCの辺にそって離れることなく三角形ABCの内側を一周させたとき,円Pの中心が動いてできる線の中で,BCと平行な部分の長さを求めなさい。
② 三角形ABCの面積を求めなさい。
➤➤➤解説
難しい問題です。どこから手を付けていいか悩みますね。
三角形DEFすらかかれていませんから、まずは問題文に書かれているように図をかいてみましょう。
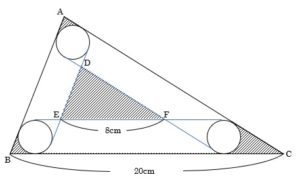
三角形ABCと三角形DEFが相似であり、相似比が20:8=5:2ということは分かります。
ですが、これだと何も解決しません。
そこで、それぞれの三角形に内接する円をかいてみて、そこから解決策を探しましょう。
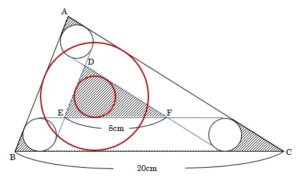
円が内接する三角形の相似比は5:2でしたから、円の相似比(半径の比)も5:2です。
この半径の差が、半径1cmの円の直径にあたる2cm
大円の半径⑤,小円の半径②とすると差の③=2cmなのでここからそれぞれの円の半径が分かります。(大円の半径=$\frac{10}{3}$cm,小円の半径=$\frac{4}{3}$cm)
⑴ 円の中心の動いた部分を図に追加しておきましょう。
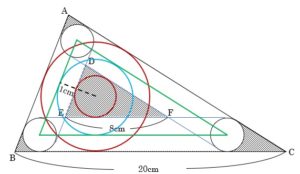
緑色の線が中心の移動した部分でできた三角形、水色の円がその内接円。
この円の半径は,$\frac{4}{3}$+1=$\frac{7}{3}$cm
円を囲む三角形の相似比は$\frac{7}{3}$:$\frac{4}{3}$=7:4なので
求める答えは8cm×$\frac{7}{4}$=14cm
ここまでで出てきたキーワード
➤ 相似,相似比,内接円,図形の内側を辺にそって円が転がる
特にこの問題では、作図と内接円から解きほぐしていくという点が重要でした。
最近多く出題される、円が三角形の内側を移動するタイプの問題では、「内接円」がポイントになっています。
⑵ 円が通過しなかった頂点A,B,Cの近くの部分をア,イ,ウとしてこれをひとつにまとめて考えます。
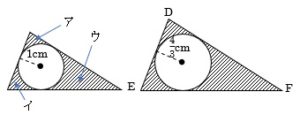
左の三角形と右の三角形の相似比は半径の比と同じで、
1:$\frac{4}{3}$=3:4
なので面積の比は3×3:4×4=9:16
2つの三角形の面積の合計は,16.86+1×1×3.14=20㎠
半径1cmの円が内接する三角形の面積がこれで分かります。
20×$\frac{9}{9+16}$=7.2㎠
半径1cmの円が内接する三角形と三角形ABCの相似比は
1:$\frac{10}{3}$=3:10
面積の比は3×3:10×10=9:100
三角形ABCの面積は7.2×$\frac{100}{9}$=80㎠
ここまでで出てきたキーワード
➤ 相似比と面積比
この問題を解くために重要な「基本事項」
三角形の内側を辺に接して円が通過する問題では、三角形の「内接円」が重要な働きをします。
内接円の考え方に慣れておかないといけませんね。
あと、相似比・面積比の考え方も当然重要でした。
相似比や面積比はどこの塾のテキストでも扱っていて、受験生は使い慣れているはずですが、内接円を使って考える問題には不慣れです。
次のテキストで練習しておきましょう。

