ほんの少しややこしい集合算かも~2020年度2日目大問2
それがこの問題です。
100人の子供たちに、ノート38冊, 鉛筆35本,消しゴム33個の文具を配ったところ,ノートだけをもらった人が19人,鉛筆だけをもらった人が18人,消しゴムだけをもらった人が15人でした。ただし,同じ文具を2つ以上もらった人はいませんでした。
⑴ ノート,鉛筆,消しゴムを1つずつ計3つもらった人は,もっとも多くて何人と考えられますか。
⑵ 文具を1つももらわなかった人は,もっとも多くて何人,また,もっとも少なくて何人と考えられますか。
⑴ ノート,鉛筆,消しゴムを1つずつ計3つもらった人は,もっとも多くて何人と考えられますか。
⑵ 文具を1つももらわなかった人は,もっとも多くて何人,また,もっとも少なくて何人と考えられますか。
➤➤➤解説
まずはベン図にまとめる
集合算的な問題なので、ベン図にまとめてみます。
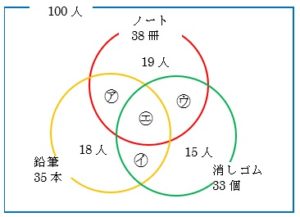
図のようにノートだけ、鉛筆だけ、消しゴムだけもらった人数を
該当箇所に書きこみます。
さらに表に整理して条件を整理する
3つの円の交わり方は図のようになるはずなので、
その交わっている部分に、便宜上㋐~㋓と記号を入れましょう。
すると
㋐+㋓+㋒=38-19=19人
㋐+㋑+㋓=35-18=17人
㋑+㋒+㋓=33-15=18人
と分かります。
これを表にすると次の通り。
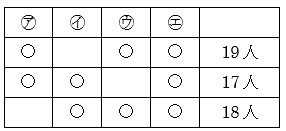
方程式ならば、未知数4つで式が3つなので、解は1つに決まらないパターンです。
(数学でいう「不定方程式」の1種ですね)
ですが、算数ではこのパターンが、特に難関校では出題されることも多いですよね。
この問題では、⑴と⑵で最大とか最小とかいった条件を追加して答えをしぼっていくことになります。
⑴ ㋓が最大になるようにします。
㋓=17人のとき㋐=㋑=0人になるが、㋒が2か1となって決まりません。
㋓=16人のとき,㋐+㋒=3人,㋐+㋑=1人,㋑+㋒=2人より
㋐=1人,㋑=0人,㋒=2人
ですから、最大は16人で決まりです。
(㋐,㋑,㋒の3つのうち2つずつの和が決まれば、和差算や消去算でサクサク答えを求められないといけません。)
⑵ ㋓が最大のとき、1つももらえない人も最大になります。
100-(38+18+15)=29人
次に、㋓が最小のとき1つももらえない人が最小になります。
㋓=0人のとき㋐=9人,㋑=8人,㋒=10人
100-(38+18+15+8)=21人
このように、ベン図にまとめたものを、さらに表に整理することで
考えもまとまりやすいですね。
ここまでで出てきたキーワード
答えが1つに決まらない(不定方程式的な)問題
集合算とベン図
3つの数の和差算・消去算
どれも必須の課題ですね。

