東大寺2025年度算数 大問4

「東大寺の算数を解いてみた」シリーズ。
今回は、2025年度入試問題から大問4。反射の問題です。

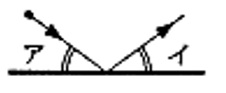
1辺の長さが64mの正方形ABCDがあり，辺AB上の点Pから辺BC上の点Qに向けて球を打ち出します。球は辺に当たるまで正方形の内部をまっすぐ進み，辺に当たると図のようにアとイの角度が等しくなるようにはね返ります。また，球が辺ではね返るたびに球の速さは\(\frac{2}{3}\)倍になり，それ以外のところでは球の速さは変化しません。
打ち出してから初めてPに戻ってくるまでの球の動きについて，次の問いに答えなさい。
ただし，球の大きさは無視します。また，球が正方形の頂点に行くような経路は考えません。

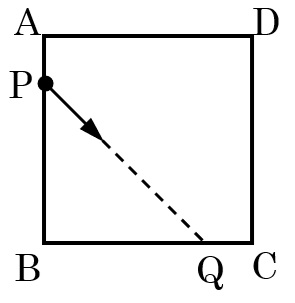
⑴　BPとBQの長さをともに48mとして球を打ち出したところ，球がQに当たるまでに48秒かかりました。
①　球がQに当たってから辺CDに当たるまでの時間は何秒ですか。
②　球を打ち出してから辺CDに当たるまでの時間と，球が辺CDに当たってからPに戻ってくるまでの時間の比を，最も簡単な整数の比で表しなさい。

三角形PBQは直角二等辺三角形で、BP＝BQ＝48mなので、QC＝64－48＝16m
図1のように点Rを取れば、CR＝12mで、三角形QCRも直角二等辺三角形。
2つの三角形は相似で、相似比は48：16＝3：1

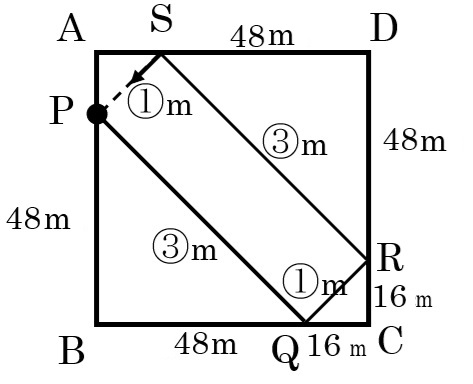
①　球がQに当たってから辺CDに当たるまでの時間
PQ：QR＝3：1で、それぞれを進む速さの比は1：\(\frac{2}{3}\)＝3：2
よって、PQとQRを進むのにかかる時間の比は、3÷3：1÷2＝2：1なので、球がQに当たってから辺CDに当たるまでの時間は、48×\(\frac{1}{2}\)＝24秒
②　球を打ち出してから辺CDに当たるまでの時間と，球が辺CDに当たってからPに戻ってくるまでの時間の比
AD上で球があたる点をSとする。
PQ，QR，RS，SPを球が進む速さの比は1：1×\(\frac{2}{3}\)：1×\(\frac{2}{3}\)×\(\frac{2}{3}\)：1×\(\frac{2}{3}\)×\(\frac{2}{3}\)×\(\frac{2}{3}\)＝27：18：12：8
PQ，QR，RS，SPの長さの比は3：1：3：1
→　それぞれかかる時間の比は、3÷27：1÷18：3÷12：1÷8＝\(\frac{1}{9}\)：\(\frac{1}{18}\)：\(\frac{1}{4}\)：\(\frac{1}{8}\)＝8：4：18：9なので、
(8＋4)：(18＋9)＝4：9

⑵　BPとBQの長さを等しくして，⑴と同じ速さで球を打ち出したところ，球がPに戻ってくるまでに273秒かかりました。
①　球を打ち出してから辺CDに当たるまでの時間は何秒ですか。
②　BPの長さを求めなさい。

①　球を打ち出してから辺CDに当たるまでの時間
図で、PQ＝RSなので、かかる時間の比は速さの逆比。
PQ上の速さを1とすると、RS上の速さは、1×\(\frac{2}{3}\)×\(\frac{2}{3}\)＝\(\frac{4}{9}\)なので、かかる時間の比は4：9
→　PQ間を④秒、RS間を⑨秒とする。
同様に、QR間を❹秒、SP間を❾秒とする

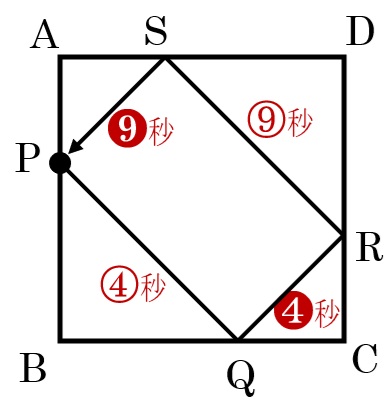
④＋❹＋⑨＋❾＝273秒なので、⑬＋⓭＝273秒
①＋➊＝21秒
よって、CDに当たるまでの時間は、④＋❹＝21×4＝84秒　

②　BPの長さ
BPの長さが1m減るとPQは[1]長さが減り、逆にQRが[1]増える。
BP間では[1]で1秒かかるが、QR間では[1]で1秒×\(\frac{3}{2}\)＝1.5秒かかる。

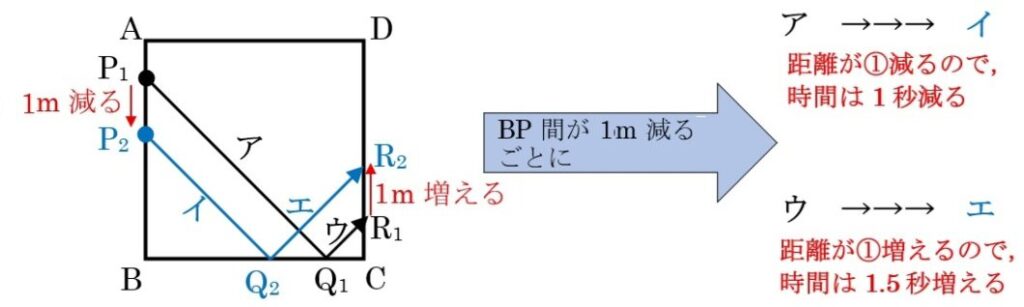
⑴から、BPが48mのとき、CDに到達するのにかかる時間は48＋24＝72秒
BPが1m減るごとに時間は1.5－1＝0.5秒増えていくので、
(84－72)÷0.5＝24より、BPが48mのときから24m減ったことになる。
だから、このときのBPの長さは
48－24＝24m

⑶　BPの長さを16m，BQの長さを32mとして，ある速さで球を打ち出したところ，球がPに戻ってくるまでに490秒かかりました。球を打ち出してからQに当たるまでの時間は何秒ですか。

正確に図を描きましょう。

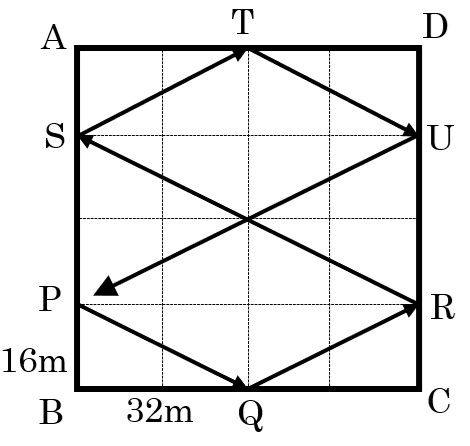
16mは1辺64mの4等分点の1つで、32mは2等分点なので、できるだけ正確に図を描けば上のようになる。
移動した距離の比は
PQ：QR：RS：ST：TU：UP＝1：1：2：1：1：2
それぞれの進む速さの比は
PQ：QR：RS：ST：TU：UP＝1：\(\frac{2}{3}\)：\(\frac{4}{9}\)：\(\frac{8}{27}\)：\(\frac{16}{81}\)：\(\frac{32}{243}\)
「距離の比÷速さの比＝かかる時間の比」なので、それぞれを進む時間の比は
1÷1：1÷\(\frac{2}{3}\)：2÷\(\frac{4}{9}\)：1÷\(\frac{8}{27}\)：1÷\(\frac{16}{81}\)：2÷\(\frac{32}{243}\)＝16：24：72：54：81：243
この合計が490秒なので、
球を打ち出してからQに当たるまでの時間は、
490×\(\frac{16}{16＋24＋72＋54＋81＋243}\)＝16秒

究学からのご案内

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。

➪2024年度大阪星光算数入試問題と解説、見本を無料進呈しています。