東大寺2024年度算数 大問3

「東大寺の算数を解いてみた」シリーズ。
今回挑戦するのは、2024年度の大問3。立体図形の問題ですが、何と立方体を3方向からくり抜く問題です。なんか強敵感を強く感じる一題ですな。

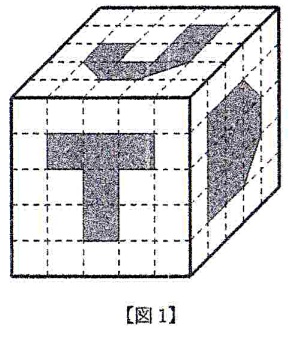
一辺の長さが10cmの立方体の3つの面の一部分に，下の [図1]，[図2] のように色をつけます。そして，色をつけた部分をその面から向かい合う面までまっすぐくりぬいて穴をあけ，くりぬいた部分を取り除いて新しい立体を作ります。このとき，次の問いに答えなさい。ただし，各面の点線は2cmの間隔で引かれています。
⑴　[図1] のように色をつけた場合にできる立体の体積を求めなさい。

段ごとにしらべていく方法がいいでしょうね。
5段分の，5×5のマスに区切った正方形を上から順に、1段目，2段目，…，5段目とします。
これに真上から見て抜き取られる部分（5段とも同じになる）に色をつけ、次に縦方向にくりぬく部分に上向きの矢印（↑），横方向にくりぬく部分に左向きの矢印（←）を記入。
その際、斜めに切断されて半分だけ残る部分が分かるようにしておきましょう。
この作業がきちんとできたら、記入した矢印にしたがって、くりぬく部分に色をつけます。

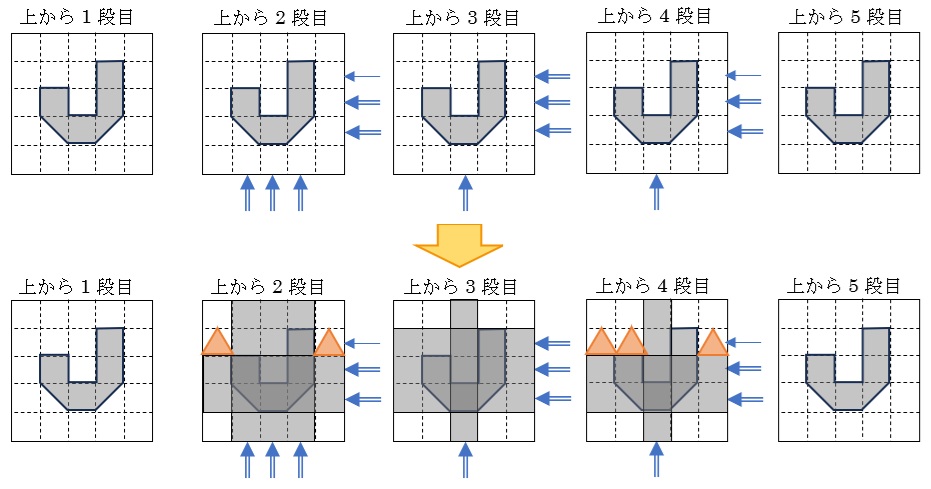
1段目から順に、色のついていない1辺2cmの立方体の個数を数えましょう。
1段目…20個，2段目…4＋0.5×2＝5個，3段目…8個，4段目…8＋0.5×3＝9.5個，5段目…20個
以上を合計すると、20＋5＋8＋9.5＋20＝62.5個なので、体積は2×2×2×62.5＝500cm³です。

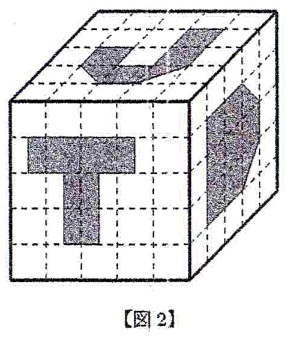
⑵　[図2] のように色をつけた場合にできる立体の体積を求めなさい。ただし，[図2] の正面から見た面の色のついている部分は，[図1] の正面から見た面の色のついている部分を左へちょうど1cmずらしたものです。

⑴と同じ手順で段ごとの図を描きましょう。

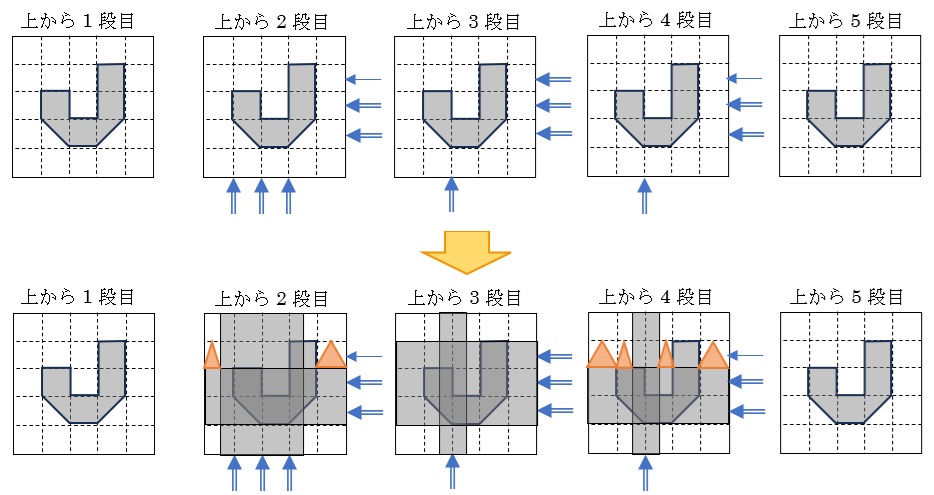
⑴と同じように数えます。
1段目…20個，2段目…4＋0.5＋0.25＝4.75個，3段目…8個，4段目…8＋0.5×2＋0.25×2＝9.5個，5段目…20個
以上を合計すると、20＋4.75＋8＋9.5＋20＝62.25個なので、体積は2×2×2×62.25＝498cm³です。

思ったより簡単でした。試験中は、焦らずきちんと図を描いて、丁寧にやれば得点できる問題ですね。

究学からのご案内

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。

➪2024年度大阪星光算数入試問題と解説、見本を無料進呈しています。