東大寺2025年度算数 大問1

「東大寺の算数を解いてみた」シリーズ。
2025年度大問1は、小問が⑴～⑷の4題で、うち計算問題が⑴と⑵の2題。
ともかく、解いてみましょう。

次の各問いに答えなさい。（解答欄には答えのみ記入しなさい。）
⑴　次の計算をしなさい。
　　\(\frac{1}{3}\)＋\(\frac{36}{7}\)×4.25－\(\frac{5}{8}\)÷0.525

計算問題を解くときは、できるだけ「計算しない」方針で行くと時間も短縮できてミスも減らせます。
え？どういうこと？
では実際にやってみて、種明かしを。
\(\frac{36}{7}\)×4.25＝\(\frac{36}{7}\)×\(\frac{17}{4}\)＝\(\frac{9×17}{7}\)
\(\frac{5}{8}\)÷0.525＝\(\frac{5}{8}\)×\(\frac{1000}{525}\)＝\(\frac{25}{21}\)
\(\frac{1}{3}\)＋\(\frac{9×17}{7}\)－\(\frac{25}{21}\)＝\(\frac{7}{21}\)＋\(\frac{9×17×3}{21}\)－\(\frac{25}{21}\)＝\(\frac{7＋9×17×3－25}{21}\)
9×17×3は計算しなかったけど、ここではやっておかないとですね。
9×17×3＝459
なので、\(\frac{7＋9×17×3－25}{21}\)＝\(\frac{7＋459－25}{21}\)＝\(\frac{441}{21}\)＝21でこれが答え。
この問題では途中でかけ算の答えを出さなかった。ま、この場合はかけ算の答えを途中で出していても大差なかったかも、でした(;^_^A

⑵　次の計算をしなさい。
　　\(\frac{85}{7}\)÷(\(\frac{25}{8}\)－\(\frac{31}{14}\))＋\(\frac{17}{56}\)÷(\(\frac{25}{16}\)－\(\frac{31}{28}\))

\(\frac{25}{8}\)－\(\frac{31}{14}\)＝\(\frac{175}{56}\)－\(\frac{124}{56}\)＝\(\frac{51}{56}\)
\(\frac{25}{16}\)－\(\frac{31}{28}\)＝\(\frac{175}{112}\)－\(\frac{124}{112}\)＝\(\frac{51}{112}\)
\(\frac{85}{7}\)÷\(\frac{51}{56}\)＋\(\frac{17}{56}\)÷\(\frac{51}{112}\)
＝\(\frac{85×56}{7×51}\)＋\(\frac{17×112}{56×51}\)
＝\(\frac{40}{3}\)＋\(\frac{2}{3}\)
＝14
ミスできない問題でした。

⑶　504を100で割ると，商が5であまりが4となります。このように，100で割ったときの商があまりの\(\frac{5}{4}\)倍となるような整数のうち，最も大きいものを求めなさい。

商とあまりの比は5：4なので、あまりは4の倍数。
また、100で割っているので、あまり（整数）は最も大きい場合でも99。
ですから、あまりは99以下の4の倍数で、もっとも大きいのは96
このとき商は、96×\(\frac{5}{4}\)＝120
□÷100＝120あまり96
よって、求める整数は、100×120＋96＝12096

⑷　下の図は，半径が6cmである円の周を12等分して点を打ったものです。塗りつぶされている部分の面積の和を求めなさい。

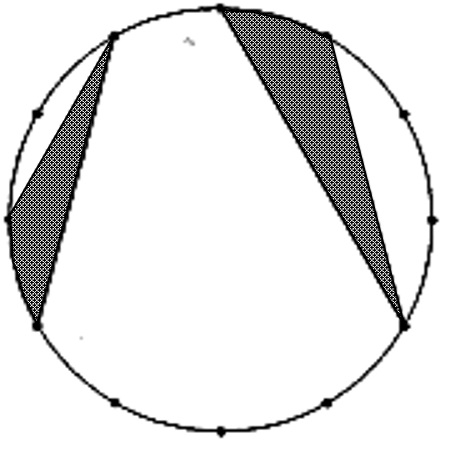
円に絡んだ面積なので、円の中心を意識して解く必要があります。
その前に、この問題では2つの部分をひとつにできるので、そこからやっておきましょう。

まず、図アのように、左側の部分を右に移動します。
次に、図イのように円の中心Oと図の点Cを通る直径を記入すると、OCとABは平行になります。
なので、三角形ABCは形を変えて三角形ABOになっても面積は同じです。
ですから、色のついた部分はおうぎ形OABの面積と同じです。中心角は60度、半径は6cmなので、
6×6×3.14×\(\frac{1}{6}\)＝18.84cm²になります。

究学からのご案内

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。

➪2024年度大阪星光算数入試問題と解説、見本を無料進呈しています。