東大寺2014年度算数 大問2

「東大寺の算数を解いてみた」シリーズ。
2014年度大問2をやってみましょう。

水平な地面の上に地点A，Cがあり，地点Cの真上には光源があります。長さ1.5mの棒を水平な地面に対してつねに垂直に立てて，棒の影の長さを測りました。地点Aでは３．６ｍで地点Ａから地点Ｃの方向へ3m離れた地点Bでは1.8mでした。
また，地点Cから地点Fまでは，傾きが一定の上り坂が続き，地点Cから地点Fの方向へ少し上った地点Dでは，影の長さは3.6mでした。さらに地点DからCD間の距離の1.5倍の距離を地点Fの方向へ上った地点Eでは，棒の上端と地点Fが同じ高さとなり，そのときの棒の影の先端は，地点Fから地点Eの方向へ0.5m離れた地点にありました。このとき，次の問いに答えなさい。

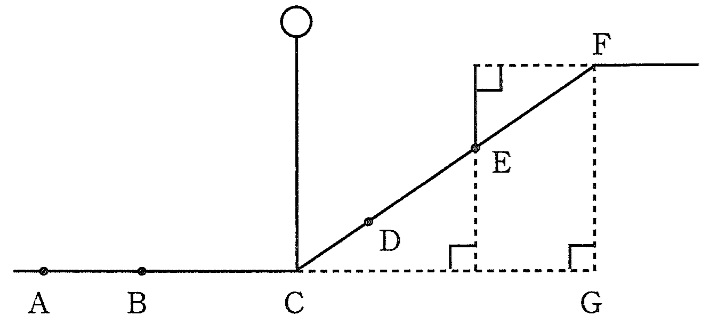
⑴　AC間の距離は何mですか。
⑵　光源の高さは何mですか。

⑴と⑵をまとめてやってみよう。
1つ目の方法

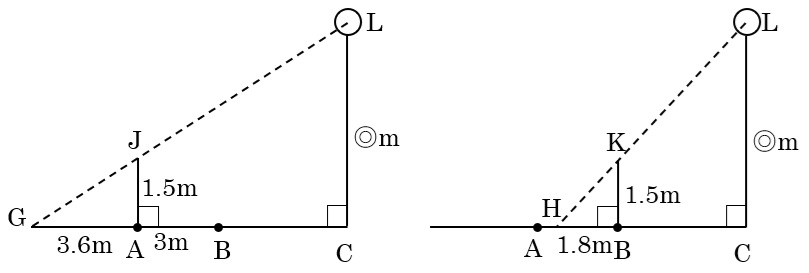
A地点に棒を立てた図とB地点に棒を立てた図を比べます。
GA：GC＝1.5：◎，HB：HC＝1.5：◎でGA＝3.6m，HB＝1.8mなので、GA：HB＝2：1より
GC：HC＝2：1となり、AC：BC＝2：1
（少し分かりづらいが、左の図は右の図を横に2倍引き延ばしているイメージだ。）
ACとBCの差は3mなので、AC＝3m×2＝6mとなります。
次に左の図で（右の図で考えてもいい）三角形LGCと三角形JGAはピラミッド相似で、相似比は3.6：(3.6＋6)＝3：8より、光源の高さLC(◎)＝1.5×\(\frac{8}{3}\)＝4m
悪いやり方じゃないけど、少し分かりにくいかも…

2つ目の方法

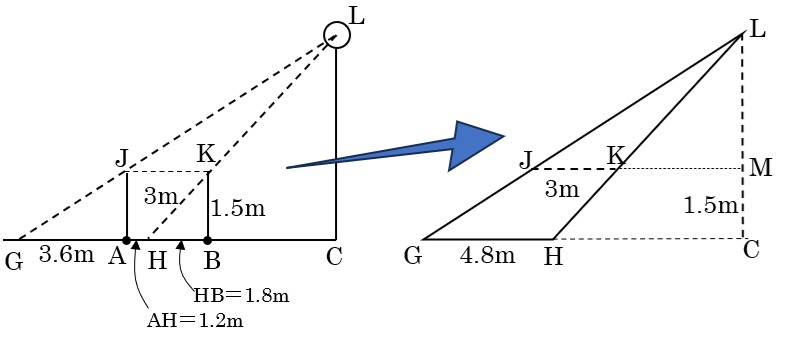
分かる長さを必要な部分に書き込んでいくと、左の図のようになる。
ここから三角形LGHを抜き出して考えよう。
三角形LGHと三角形LJKは相似で、相似比は4.8：3＝8：5
よって、LC：LM＝8：5となり、光源の高さLC＝1.5×\(\frac{8}{8－5}\)＝4m
また、左側の図の三角形HCLに注目すると、三角形HCLと三角形HBKはピラミッド相似。
相似比は4：1.5＝8：3なので、HC＝1.8×\(\frac{8}{3}\)＝4.8m
AC＝4.8＋1.2＝6m
このやり方だと、先に⑵の答えが出るが、ボクはこちらが好みだ。

⑶　水平な地面からの地点Fの高さ（図FGの長さ）は何mですか。

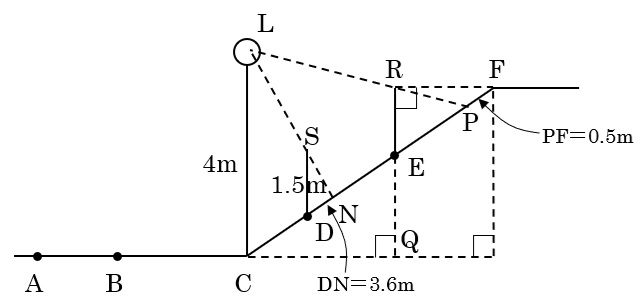
今度は、CLの右側を使って、
三角形LCNと三角形SDN，三角形LCPと三角形REP（どちらもピラミッド相似），三角形FREと三角形CQE（ちょうちょ相似）を使って、順にCD，CE，PEの長さを求めていきましょう。

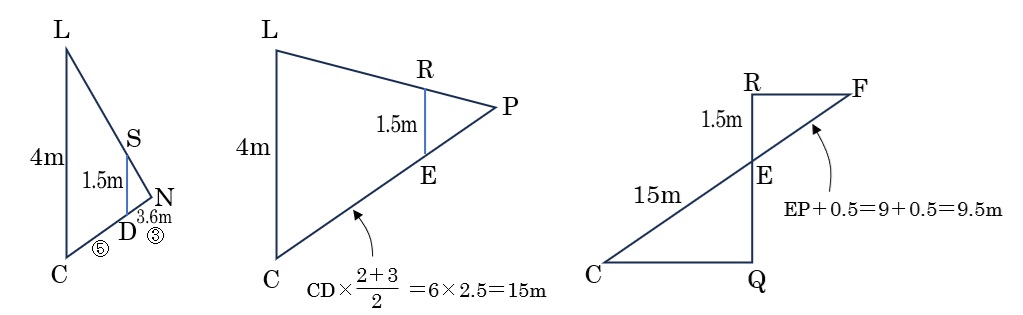
DN＝3.6mなので、CD＝3.6×\(\frac{5}{3}\)＝6m
CD：DE＝2：3なので、DE＝9mとなり、CE＝6＋9＝15m
PE：EC＝3：5なので、PE＝15×\(\frac{3}{5}\)＝9m
PF＝0.5mなので、EF＝9＋05＝9.5m
さあ、最後の仕上げです。
CE：EF＝15：9.5なので、QE：ER＝15：9.5
ER＝1.5mだから、求める高さは1.5×\(\frac{15＋9.5}{9.5}\)＝\(\frac{147}{38}\)m

究学からのご案内

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。
☆サンプルを頒布しています。詳しくはこのページまで。