東大寺2019年度算数 大問2

大問2は日暦算。出題頻度は高くないですが、きちんとやっておかないと後悔する、それが日暦算という問題です。
ともかく、実際の問題を見てみましょう。

西暦X年のカレンダーについて調べました。以下，○/△で○月△日を表すものとします。
⑴　西暦X年の2/1と8/1の曜日が同じでした。このとき，西暦X年の2/1，3/1，4/1，5/1，6/1，7/1，8/1，9/1，10/1，11/1，12/1の11日の中で，西暦X年の1/1と曜日が同じ日付を○/△の形ですべて答えなさい。

まず、平年かうるう年かが問題です。ヒントは「2/1と8/1の曜日が同じ」の部分ですね。
解き方はいろいろ考えられますが、ここでは「ぐるぐるカレンダー」を使ってやってみましょう。
下の図で◎は日～土を表しています。

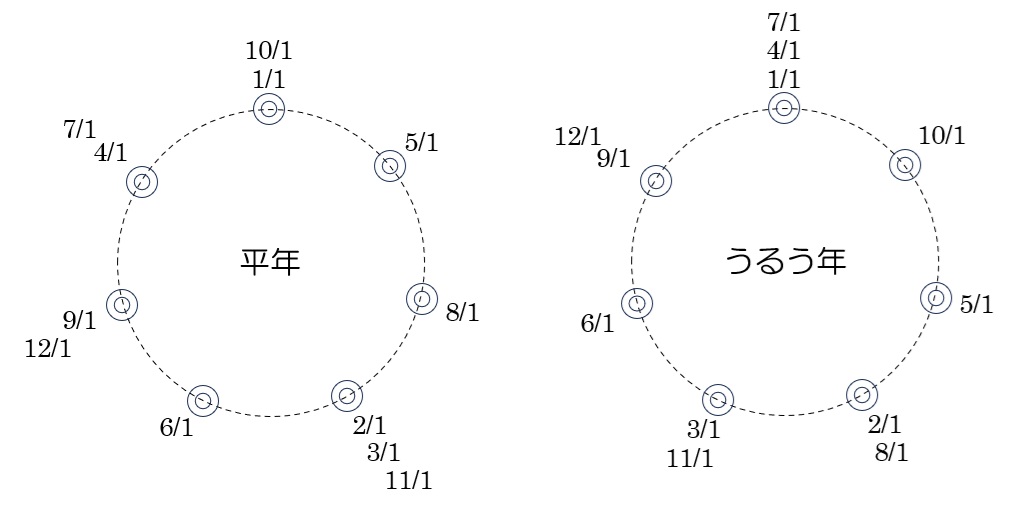
2/1と8/1の曜日が同じになっているのは、うるう年ですから、こちらで考えます。
1/1と同じ曜日は、右側のぐるぐるカレンダーを見て分かる通りで、4/1と7/1です。

⑵　西暦X年6月のすべての水曜日の日にちの合計は65以下でした。このとき，西暦X年の6/1の曜日として考えられるものをすべて答えなさい。

各月に水曜日は4回か5回あります。
4回の場合
　→　第1水曜を①日とすると、4回分は①＋(①＋7)＋(①＋14)＋(①＋21)＝④＋42
5回の場合
　→　第1水曜を①日とすると、5回分は①＋(①＋7)＋(①＋14)＋(①＋21)＋(①＋28)＝⑤＋70
合計が65以下なので、4回だと分かります。
④＋42≦65より、④≦23なので、①＝1，2，3，4，5ですが、1～2の場合、第5水曜があることになりますから、①＝3か4か5、つまり第1水曜日は6/3，6/4，6/5のどれかです。
6/3が水曜日の場合　→　6/1は月曜日
6/4が水曜日の場合　→　6/1は日曜日
6/5が水曜日の場合　→　6/1は土曜日
ですから、答えは、土曜日、日曜日、月曜日となります。

⑶　⑴，⑵のとき，さらに西暦X年10月のすべての月曜日の日にちの合計は70以上でした。
①　西暦X年の1/1は何曜日ですか。

⑵で使った考え方を再度使います。月曜日の回数は4回か5回です。
4回の場合
　→　第1水曜を①日とすると、4回分は①＋(①＋7)＋(①＋14)＋(①＋21)＝④＋42
5回の場合
　→　第1水曜を①日とすると、5回分は①＋(①＋7)＋(①＋14)＋(①＋21)＋(①＋28)＝⑤＋70
④＋42≧70なので④＝28より，①＝7
⑤＋70≧70，①＋28≦31なので①＝1，2，3
それぞれ調べましょう。このとき、⑵の6月と整合性が取れないといけません。（上のぐるぐるカレンダーで調べたら分かります。）
10/7が月曜日の場合　→　10/1は火曜日　→　6/1は土曜日　⇦　オーケー
10/1が月曜日の場合　→　　　　　　　　 →　6/1は金曜日　⇦　ダメ
10/2が月曜日の場合　→　10/1は日曜日　→　6/1は木曜日　⇦　ダメ
10/3が月曜日の場合　→　10/1は土曜日　→　6/1は水曜日　⇦　ダメ
以上から、6/1は土曜日なので、1/1は月曜日となります。

②　西暦X年の翌年の、1/1，2/1，3/1，4/1，5/1，6/1，7/1，8/1，9/1，10/1，11/1，12/1の12日の曜日の中で最も多くあるのは何曜日ですか。

西暦X年の1/1が月曜日と分かったので、翌年の1/1は、2日分の曜日がずれて、水曜日です。
上のぐるぐるカレンダーの左が平年の図なので、これを使いましょう。

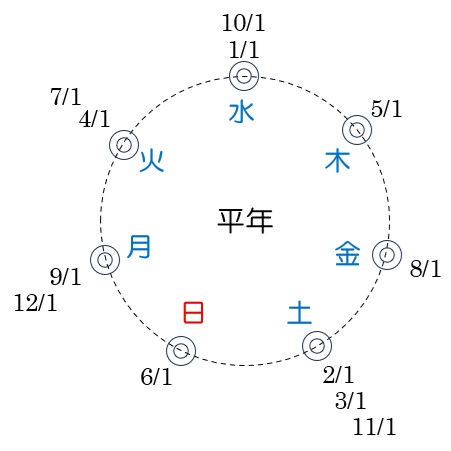
土曜日が3回あるので、これが最も多いですね。答えは土曜日です。

今回は、ぐるぐるカレンダーで考えました。
1年は1週間の日～土のくり返し。月が替わるときに、曜日は0日～3日ずれていくのを利用した図です。
（細かく書けば、月末が28日のときには0日、月末が29日のときには1日、月末が30日のときには2日、月末が31日のときには3日ずれます。）

簡単ではないですが、できれば全問正解を狙いたい問題です。

以下は究学からのおすすめです。

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。