東大寺2019年度算数 大問3

2019年度東大寺学園算数の解説をやってみました。
いやー、それにしても難しい…
受験生がこれらの問題をわずか60分で合格点に仕上げるのって、けっこう大変なんだろうなぁと、あらためて感じているところです。満点は必要なくても、悪くても6割5分、ふつうであれば7割はとっておかないと合格ラインに食い込めないですからね。

というわけで、とりあえず解説をスタートしましょう。
2019年度の大問3⑴です。

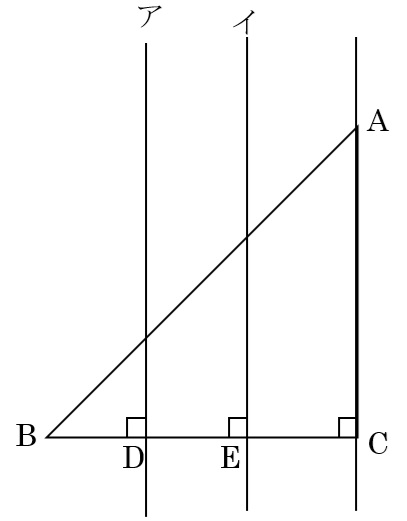
下の図において，三角形ABCは直角二等辺三角形で，AC＝BC＝9cmです。BCを三等分している点をBに近い方からD，Eとし，Dを通りBCに垂直な直線をア，Eを通りBCに垂直な直線をイとします。
①　三角形ABCを直線アのまわりに1回転してできる立体の体積は，三角形ABCをACのまわりに1回転してできる立体の体積の何倍ですか。

ACを回転の軸とするときの体積は
9×9×π×9×\(\frac{1}{3}\)＝9×9×3×π(cm³)　…㋐
アを回転の軸とするときの体積は、半径6cmで高さが9cmの円柱から，底面の半径6cmで高さ6cmの円すいを引いて求めるので
6×6×π×9－6×6×π×6×\(\frac{1}{3}\)＝6×6×7×π(cm³)　…㋑

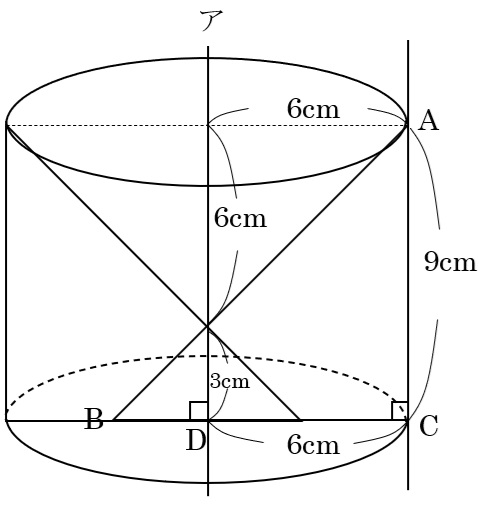
㋑は㋐の何倍かを求めるので、
㋑÷㋐＝(6×6×7×π)÷(9×9×3×π)＝\(\frac{6×6×7×π}{9×9×3×π}\)＝\(\frac{28}{27}\)倍

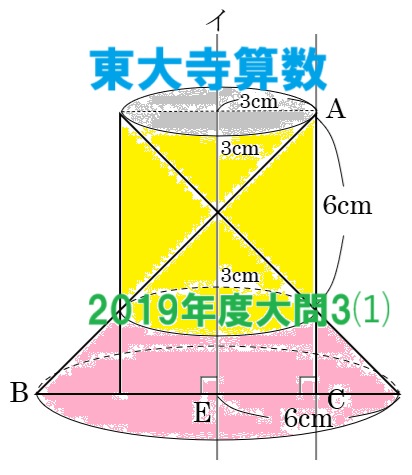
②　三角形ABCを直線イのまわりに1回転してできる立体の体積は，三角形ABCをACのまわりに1回転してできる立体の体積の何倍ですか。

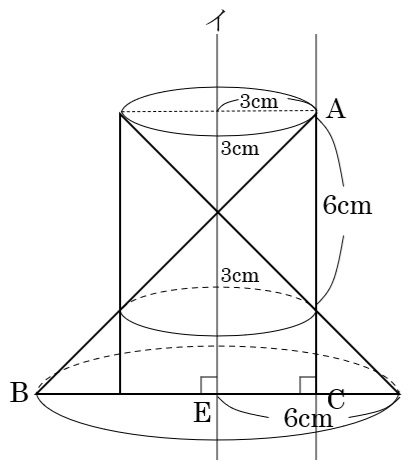
イを回転の軸とするときの体積は
底面の半径6cm，高さ6cmの円すいから底面の半径3cm，高さ3cmの円すいを引いた体積（円すい台㋒）＋底面の半径3cm，高さ6cmの円柱の体積（㋓）－底面の半径3cm，高さ3cmの円すい（㋔）
で求める。
㋒　6×6×π×6×\(\frac{1}{3}\)－3×3×π×3×\(\frac{1}{3}\)＝63×π
㋓　3×3×π×6＝54×π
㋔　3×3×π×3×\(\frac{1}{3}\)＝9×π
㋒＋㋓－㋔＝108×π
①より、㋐は243×π
ですから、(108×π)÷(243×π)＝\(\frac{108×π}{243×π}\)＝\(\frac{4}{9}\)倍

東大寺にしては素直な問題なので、受験生は絶対にミスできません。
きちんと図を描いて、式を丁寧に作り、計算間違いなどしないようにやっていきましょう。

以下は究学からのおすすめです。

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。