「東大寺の算数を解いてみた」シリーズ。
2014年度大問1⑶の速さの問題です。
それなりに難しいかも、です。
ある池のまわりの道を,A君は自転車で,B君は徒歩で,それぞれ一定の速さで回ります。A君は,午前9時にある地点Pを出発し,午前10時に池のまわりをちょうど5周回って地点Pを通過しました。B君は,午前9時4分に地点PをA君とは反対向きに出発しました。2人が3回目に出会ったのは午前9時30分でした。2人が最初に出会ったのは午前9時何分何秒でしたか。
A君が5周するのにかかった時間はちょうど1時間=60分ですから、1周にかかる時間は12分です。
B君が出発したとき、A君は池のまわりを\(\frac{1}{3}\)(12分で1周するうちの4分の分)進んでいます。
池1周の長さを[12]とすると、出会うのにかかる時間の比は
(Bの出発~1回目の出会い):(1回目の出会い~2回目の出会い):(2回目の出会い~3回目の出会い)
=[8]÷速さの和:[12]÷速さの和:[12]÷速さの和
=2:3:3 → ②分,③分,③分とする
②+③+③=⑧が26分なので、②=6.5分,つまり初めて出会ったのはB君が出発してから6.5分後です。9時4分+6.5分=9時10.5分
つまり、2人が最初に出会ったのは午前9時10分30秒ですね。
ダイヤグラムを利用して解くという方法もありますよ。
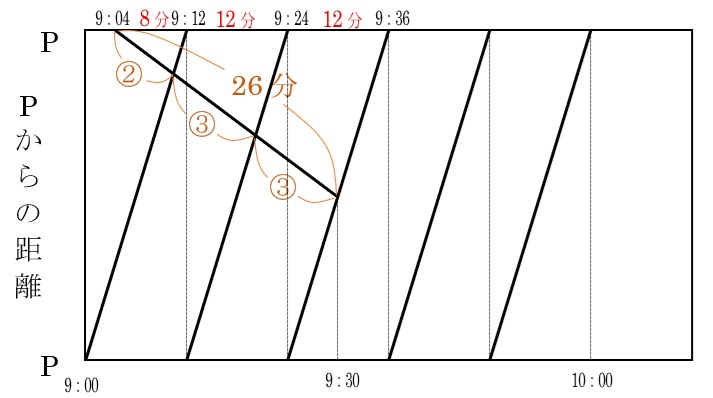
上の図で⑧=26分なので、②=6.5分
これで答えに直結ですね。
究学からのご案内
大阪星光を目指すなら
大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。
➪2024年度大阪星光算数入試問題と解説、見本を無料進呈しています。
オンライン個別指導で算数・国語も実力伸長!
算国オンライン個別指導塾究学の生徒も募集しています(年中いつでも歓迎します。まずは無料体験で)



