東大寺の2018年度大問1の⑶は立体図形の問題です。
さっそく見てみましょう。
立体㋐は各面の対角線(例えばAB)の長さが2cmの立方体,立体㋑は4つの面がすべて1辺の長さが2cmの正三角形である三角すい,立体㋒は底面が1辺の長さが2cmの正方形で,4つの側面がすべて1辺の長さが2cmの正三角形である四角すいです。立体㋑の体積,立体㋒の体積は,立体㋐の体積のそれぞれ何倍ですか。
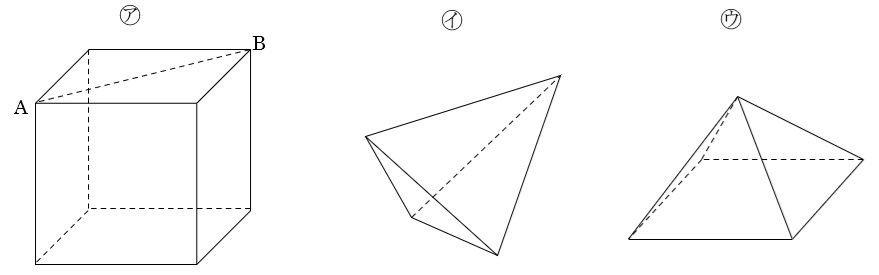
立方体の体積は求められないし、一見すると難しく思えます。
ですが・・・
㋑は㋐の立方体をもとに、4つの頂点をふくむ三角すいを切断することで作ることができます。
下の図で、まず頂点A,B,Cを通る面で頂点Pをふくむ三角すいを切断します。
この三角すいの体積はもとの立方体の体積の\(\frac{1}{6}\)です。
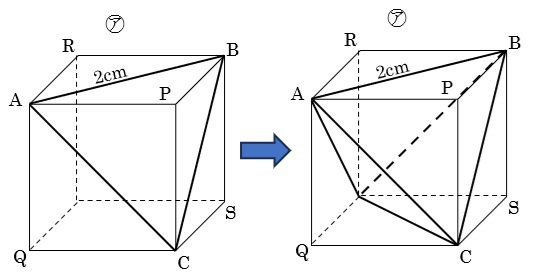
引き続き、頂点Q,頂点R,頂点Sをふくむ三角すいを次々と切断すれば、立体㋑の完成です。
ですから㋑の体積は㋐から\(\frac{1}{6}\)の三角すいを4個取り去ることになるので、
1-\(\frac{1}{6}\)×4=\(\frac{1}{3}\)となります。
㋒は、そのままの立体を㋐の中に作ることができないようです。
ですが、図のように立方体の各面の対角線の交点H,I,J,K,L,Mを結んでできる立体(正八面体)から考えることができます。

6つの点をとなり合った面の点どうし結ぶと、下の図1のような正八面体ができます。
立体㋒はこの正八面体の上半分の立体と相似です。
図2より、1辺の長さは対角線ABの半分で1cm。
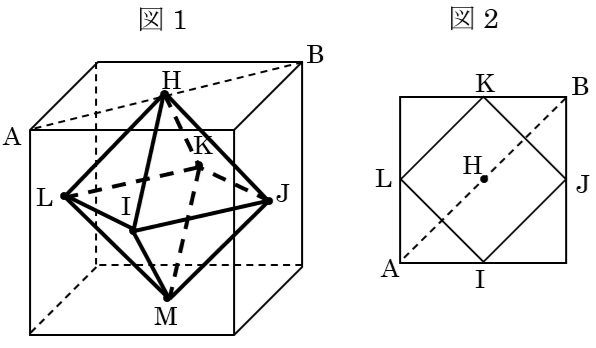
ここにできた正八面体の体積はもとの立方体㋐の体積の\(\frac{1}{2}\)×1×\(\frac{1}{3}\)=\(\frac{1}{6}\)なので、上半分の四角すいは\(\frac{1}{6}\)×\(\frac{1}{2}\)=\(\frac{1}{12}\)
立体㋒はこの四角すいと相似で相似比は2:1なので、立体㋒の体積は
\(\frac{1}{12}\)×2×2×2=\(\frac{2}{3}\)となります。
大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
算国オンライン個別指導塾究学の生徒も募集しています(年中いつでも歓迎します。まずは無料体験で)



