東大寺2018年の大問1の⑵を見てみましょう。
問題は次の通りです。
右図の正六角形ABCDEFにおいて,AF上に点Gをとりました。三角形BCGの面積と三角形DEGの面積の比が12:13であるとき,AG:GFを最も簡単な整数の比で答えなさい。
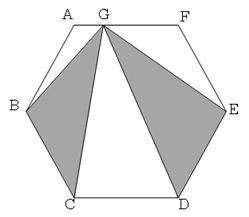
〔1〕準備
三角形ABG+三角形GEF=正六角形の\(\frac{1}{6}\)
三角形GCDは正六角形の\(\frac{1}{3}\)
⇒三角形BCG+三角形DEG=1-\(\frac{1}{6}\)-\(\frac{1}{3}\)=正六角形の\(\frac{1}{2}\)
⇒三角形BCG=\(\frac{1}{2}\)×\(\frac{12}{12+13}\)=\(\frac{6}{25}\)
〔2〕三角形BCGが正六角形の\(\frac{6}{25}\)と分かったので、これを利用する方法を2つ紹介。
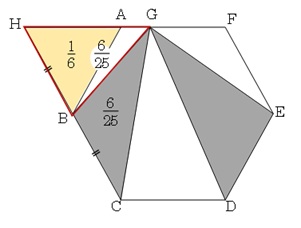
(ⅰ)正三角形ABHを追加して考える方法
図のように三角形ABHを追加する。
BC=BHなので、三角形BCG=三角形HBG=\(\frac{6}{25}\)
三角形ABH=\(\frac{1}{6}\)なので、HG:HA=\(\frac{6}{25}\):\(\frac{1}{6}\)=36:25
⇒ AG:AH=11:25 しめしめ、これで答えは出せる!GF=25-11=14
答えは,11:14 で決まり。
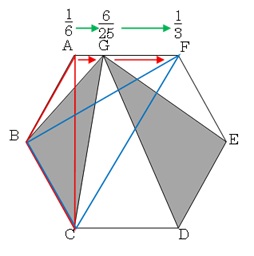
(ⅱ)変化の割合から考える方法
点GがAからFまで動く点と考える。
ア GがAにあるとき、三角形BCG=\(\frac{1}{6}\)
イ Gが問題の場所にあるとき、三角形BCG=\(\frac{6}{25}\)
ウ GがFにあるとき、三角形BCG=\(\frac{1}{3}\)
アイで\(\frac{6}{25}\)-\(\frac{1}{6}\)=\(\frac{11}{150}\)増える。
イウで\(\frac{1}{3}\)-\(\frac{6}{25}\)=\(\frac{14}{150}\)増える。
⇒ 以上から、AG:GF=\(\frac{11}{150}\):\(\frac{14}{150}\)=11:14となって答えだ。
(底辺は常にBCで一定なので、この考えが使えるのだ。)
大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
算国オンライン個別指導塾究学の生徒も募集しています(年中いつでも歓迎します。まずは無料体験で)



