東大寺2014年度算数 大問3

よく似た問題が2020年の大問3に出ていますね。

右の図のような三角形ABCと半径1cmの円Pがあります。円Pを三角形ABCの辺にそって離れることなくその内側を一周させると，三角形ABCの内部で円Pが通らなかった部分は，頂点A，B，Cの近くと中央の三角形DEFの，合わせて4つあり，その面積は全部で47.86cm²でした。次に，円Pを三角形DEFの辺にそって離れることなくその外側を一周させたところ，三角形ABCの内部で円Pが通らなかった部分の面積は全部で53.44cm²でした。このとき，次の問いに答えなさい。ただし，円周率は3.14とします。

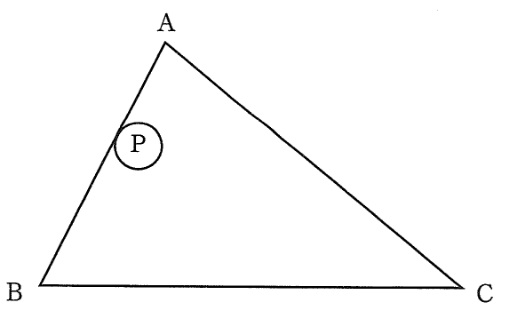
⑴①　三角形ABCの内側を一周させたときに，円Pが通らなかった4つの部分のうち，頂点Aの近くの部分を，解答欄の図に斜線で表しなさい。

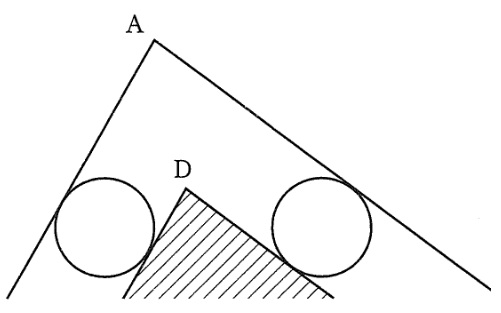
解答欄の図は上にあげたとおりです。
そして、頂点Aの近くで円が通らなかった部分は、次の通り。

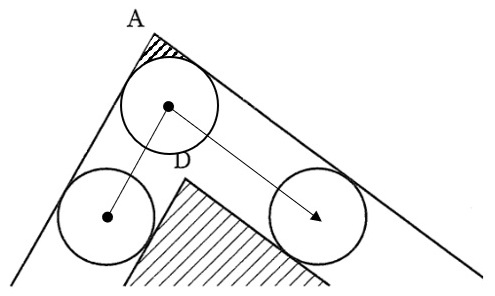
②　三角形DEFの外側を一周させたときに，円Pが通らなかった4つの部分のうち，頂点Aの近くの部分を，解答欄の図に斜線で表しなさい。

先ほどと同じ図ですが、今度は円が頂点Dを中心に回転する部分をしっかり描きます。

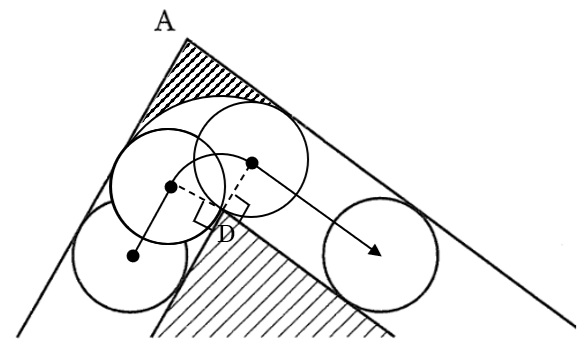
⑵　三角形DEFの面積を求めなさい。

与えられた面積は、
[1]　円Pを三角形ABCの辺にそって内側を一周させたとき，円Pが通らなかった部分は，頂点A，B，Cの近くと中央の三角形DEFで，その面積の合計は47.86cm²
[2]　円Pを三角形DEFの辺にそって外側を一周させたとき，円Pが通らなかった部分の面積の合計は53.44cm²
この2つだけです。
そこで、この2つの面積の差53.44－47.86＝5.58cm²の違いを考えましょう。
⑴の①と②の図で、斜線部分は相似です。相似比は、図の中にあるおうぎ形の半径1cmと2cmの比で1：2なので、面積の比は1×1：2×2＝1：4
この比はそのまま下の図の斜線部分の面積の比になります。

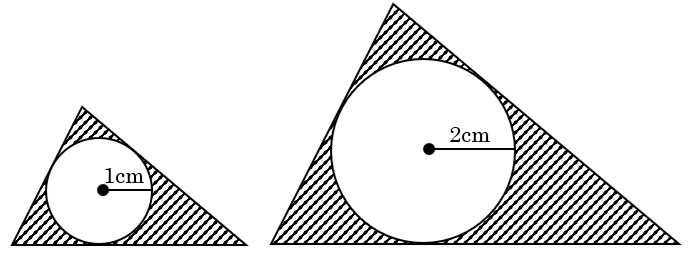
左の斜線部分の面積を①、右の斜線部分の面積を④とすると、差の③＝5.58cm²なので、
①＝1.86cm²
以上から、三角形DEFの面積は47.86－1.86＝46cm²となります。

⑶　三角形ABCのまわりの長さは,三角形DEFのまわりの長さに比べてどれだけ長いですか。

まわりの長さの差は、図の頂点A，B，C近くの斜線部分の周囲に引いた赤太線部分の長さの合計になる。

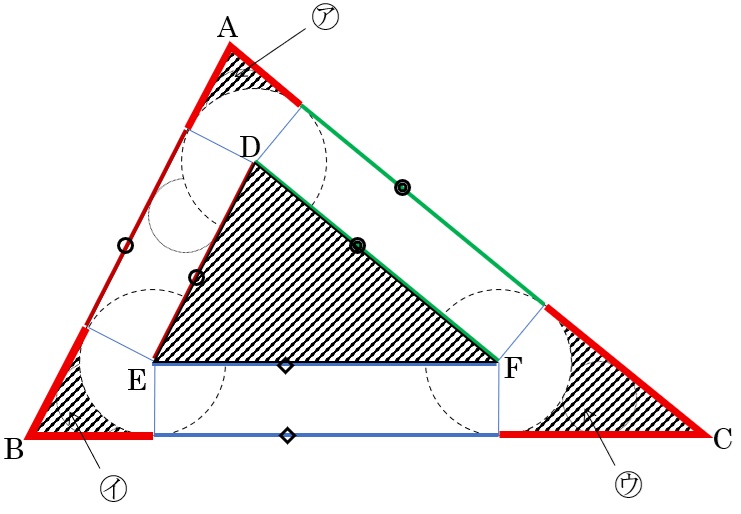
この3つの部分をひとつにまとめると、次のような三角形になる。

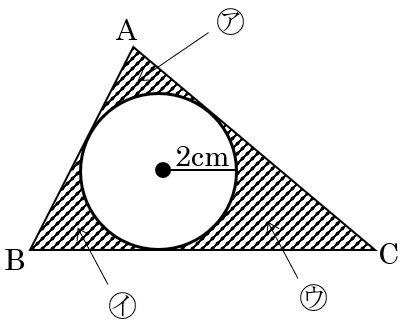
求めたい長さの差は、この三角形の周囲の長さになる。
斜線部分の面積は先の⑵より、1.86×4＝7.44cm²
これに円の面積2×2×3.14＝12.56をたせば三角形の面積になる。
7.44＋12.56＝20cm²　
上の三角形の(AB＋BC＋CA)×2÷2＝20より、
AB＋BC＋CA＝20×2÷2＝20cmでこれが答え。

究学からのご案内

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。

➪2024年度大阪星光算数入試問題と解説、見本を無料進呈しています。