東大寺2022年度算数 大問3

「東大寺の算数を解いてみた」シリーズ。
今回は2022年度大問3で、速さと図形（影の問題）の融合問題です。
あまり見かけない設定で、これは東大寺らしいといえばそうかも…

ある高層ビルの屋上には，図のような直径7mの遠州の半分と，長さ22mの直線を組み合わせた形の展望コースがあり，C地点はB地点の真東の方向にあります。身長180cmの父と身長120cmの子どもがこのコース上をA地点からC地点まで，それぞれ一定の速さで歩きます。ただし，A地点とB地点を結ぶ，図の点線は半円の直径です。円周率を\(\frac{22}{7}\)として，次の問いに答えなさい。

⑴　ある日，子どもがA地点を出発し，父がそのS秒後にA地点を出発しました。父はB地点で子供を追いこし，さらにそのT秒後にC地点に到着しました。このとき，S：T＝11：76でした。
(i)　父と子どもが歩く速さの比を，最も簡単な整数の比で答えなさい。

A～B～Cの道のりを直線で考える。
A～Bの道のりは7×\(\frac{22}{7}\)÷2＝11mで、これはB～Cの道のりの半分です。
次のような図で考えるといいでしょう。

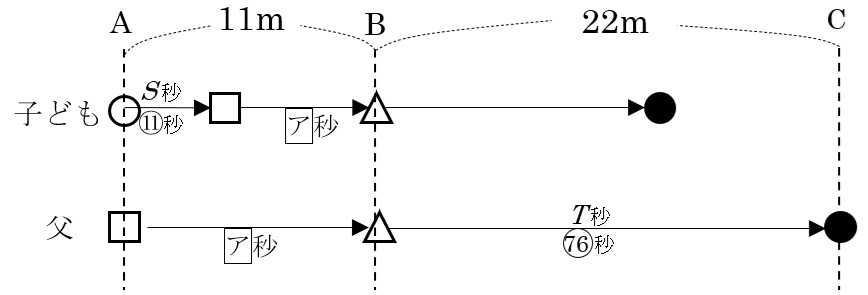
ABとBCの長さの比は11：22＝1：2なので、同じ速さで進むのにかかる時間の比も1：2
父がBC間を(76)秒で進んだので、AB間は(76)÷2＝(38)秒で進んだ。⇦図のア
同じAB間を、子どもは(11)＋(38)＝(49)秒で進んだことになります。
同じ距離を進む時間の比は、速さの比の逆比なので、父と子どもの速さの比は49：38となります。

(ii)　父が子供を追いこしてから7秒後に，太陽は真東の方向に出ており，太陽による二人の影の先端がB地点から3.2m真東の地点で重なりました。父の歩く速さは毎秒何mですか。

BC間で父と子どもの影の先端が重なったときの様子を、真横から見た図をかいて考えましょう。このとき、父も子供もB地点から7秒間進んでいます。

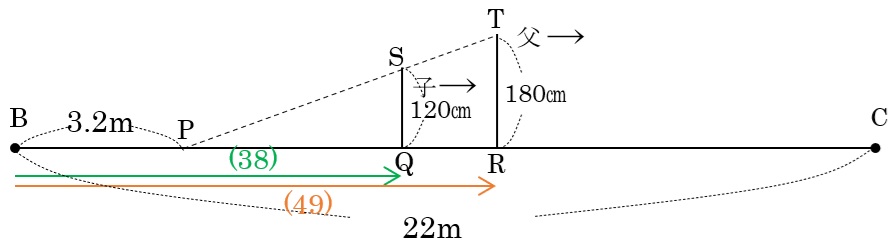
上の図で、三角形PQSと三角形PRTは相似で、相似比は120：180＝2：3
PQ＝②とすると、QR＝①＝(49)－(38)＝(11)，PQ＝(22)
BP＝3.2m＝(38)－(22)＝(16)より、(1)＝0.2m
父の秒速は(49)÷7＝(7)＝1.4より、毎秒1.4m

⑵　別のある日，子どもがA地点を出発し，その後，父がA地点を出発しました。前を行く子供がB地点を通過するまでに太陽による二人の影の先端が重なり，そのとき，子どもの影の長さは7mでした。影の先端が重なってから何秒後に父が子供を追いこしますか。ただし，二人の歩く速さは(i)(ii)の速さと等しいものとします。

影が重なったときの子どもの影の長さが7mなので、父と子どもの間の長さは7÷2＝3.5m
父のいる地点をV，子どものいる地点をW，半円の中心をOとすると、三角形VOWは正三角形になり、角VOW＝60度
このとき、父と子どものへだたり(間の道のり)は、
7×\(\frac{22}{7}\)×\(\frac{60}{360}\)m
子どもの歩く速さは父の速さの\(\frac{38}{49}\)なので、1.4×\(\frac{38}{49}\)m/秒
ですから、この後、父が子供に追いつくまでの時間は
7×\(\frac{22}{7}\)×\(\frac{60}{360}\)÷(1.4－1.4×\(\frac{38}{49}\))
＝7×\(\frac{22}{7}\)×\(\frac{1}{6}\)÷\(\frac{11}{35}\)
＝\(\frac{35}{3}\)秒となります。

計算は面倒ですが、途中でできるだけ計算せず、さいごにまとめて約分などをやれば、意外と簡単になると思います。

以下は究学からのおすすめです。

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。