東大寺2022年度算数 大問2⑶

「東大寺の算数を解いてみた」シリーズ。
今回は、2022年度大問2⑶の立体図形～切断の問題です。
2つの立体の重なる部分の体積を求めなさい、ということで、今回もけっこう多難な予感がします。

右の図の直方体ABCD-EFGHは，AB＝AD=2cm，AE＝4cmの直方体で、I，JはそれぞれBF，CGの真ん中の点です。このとき，四角すいA-IFGJと四角すいE-BIJCの重なっている部分の体積を求めなさい。(図は下の通りです。)

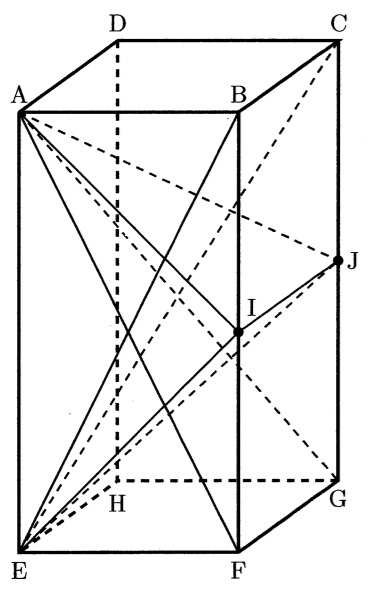
四角すいA-IFGJと四角すいE-BIJCは以下の図の通りです。

2つの立体の共通部分を考えるときに大切なことは、辺と辺の交点を調べること。
交点は次の図のようになります。

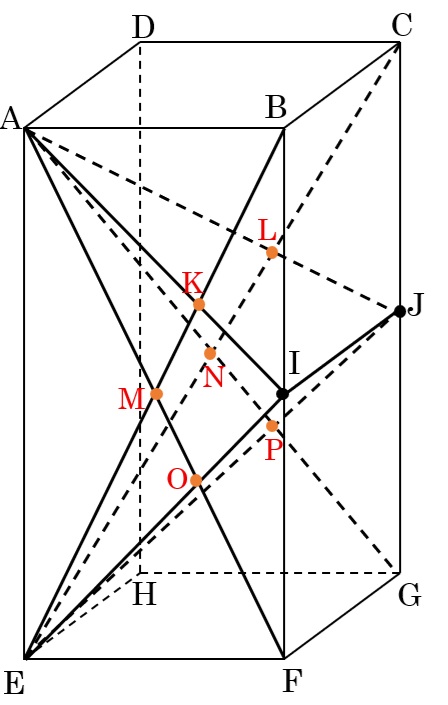
AIとBEの交点をK，AJとCEの交点をL，AFとBEの交点をM，AGとCEの交点をN，AFとIEの交点をO，AGとJEの交点をPとします。
2つの立体の共通部分は次の図の四角柱のような立体になります。

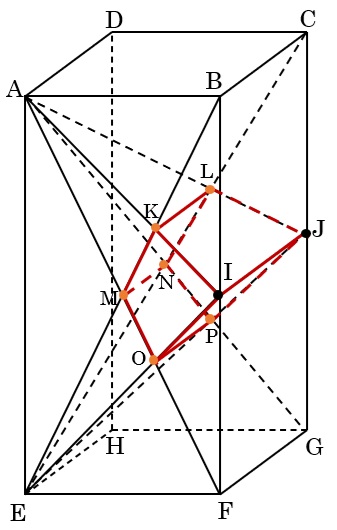
AK：KI＝2：1なので、KL＝IJ×\(\frac{2}{2＋1}\)＝2×\(\frac{2}{2＋1}\)＝\(\frac{4}{3}\)cm
AO：OF＝AE：IF＝2：1なので、OP＝2×\(\frac{2}{2＋1}\)＝\(\frac{4}{3}\)cm
MN＝1cm
また、三角形MIK＝三角形MIO＝1×(2×\(\frac{1}{2＋1}\))×\(\frac{1}{2}\)＝\(\frac{1}{3}\)cm²
求める立体の体積は、底面が三角形MIKの三角柱の斜め切断で求める体積の2倍。
よって、\(\frac{1}{3}\)×(1＋\(\frac{4}{3}\)＋2)÷3×2＝\(\frac{26}{27}\)cm³

もっと直観的に考えられるかもしれませんね。でもまあ、一応解説なので、面倒くさく仕上げました。
もちろん、この問題、簡単ではありませんよ。

以下は究学からのおすすめです。

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。