東大寺2015年度算数 大問2

「東大寺の入試問題を解いてみた」シリーズ。
今回は、2015年度の大問2、流水算の問題です。
何年かに一度、こういうガチ速さの問題が出題されていますよね。

流れのないところでの速さが等しい船A，Bがあります。A，Bは川の上流にある船着き場Pと，そこから9.1km下流にある船着き場Qとの間を何度も往復しますが，船着き場に到着するとそこで10分間停まってから再び出発するものとします。ある日の午後0時に，Aは船着き場P，Bは船着き場Qから同時に出発しました。3回目にA，Bがすれ違ったのは午後3時23分で，そこは船着き場Qから3.9kmの地点でした。このとき，次の問いに答えなさい。ただし，川の流れの速さは一定であるとします。
⑴　A，Bが2回目にすれ違ったのは午後何時何分ですか。

AとBの往復にかかる時間は同じ。
3回目にすれ違うのは、A，Bがそれぞれ1往復して、その後同時に出発し、Aが9.1－3.9＝5.2km進み、Bが3.9km進んだときなので、この船の下りと上りの速さの比は5.2：3.9＝4：3
途中の船着き場での停船時間を除くと、3回目にすれ違ったのは、最初に出発してから183分後。
Aの下りの時間：Aの上りの時間：Aが下る途中でBと出会うまでの時間
＝\(\frac{9.1}{4}\)：\(\frac{9.1}{3}\)：\(\frac{5.2}{4}\)
＝21：28：12
この合計が183分なので、最初に出発地点に戻るまでの時間は183×\(\frac{21＋28}{21＋28＋12}\)＝147分
3回目に出会ったのは、183－147＝36より、この36分後。
2回目に出会ったのはこの36分前なので、147－36＝111分後だが、2回目出会うまでに1回10分間の停船をしているので、111＋10＝121分後、つまり、午後2時1分　

⑵①　船の上りの速さと下りの速さはそれぞれ時速何kmですか。

9.1kmを下るのにかかる時間は、183×\(\frac{21}{21＋28＋12}\)＝63分なので、下りの時速は
9.1÷\(\frac{63}{60}\)＝\(\frac{26}{3}\)km　
上りの時速は、\(\frac{26}{3}\)km×\(\frac{3}{4}\)＝6.5km　

②　川の流れの速さは毎時何kmですか。

(\(\frac{26}{3}\)－6.5)÷2＝\(\frac{13}{12}\)km

➤ダイヤグラムで考える

次のようなダイヤグラムで考える方法もあります。

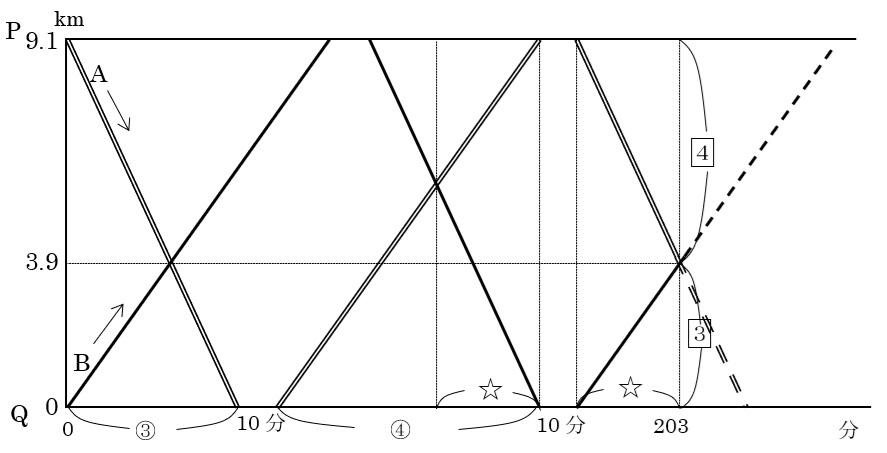
同じ時間に進んだ距離の比が4：3なので、AとBの速さの比は4：3
図の③＋④＋☆＝203分－10分×2＝183分
☆＝③×\(\frac{4}{7}\)＝\(\frac{12}{7}\)○（○で囲んだつもり・・・）
①＝183分÷(③＋④＋\(\frac{12}{7}\)○)＝21分
☆＝21×\(\frac{12}{7}\)＝36分
AがPに戻るまでの時間は
21分×(③＋④)＋10分＝157分後
よって、2回目に出会うのは157－36＝121分後　→　午後2時1分
（以下略）

ガチな速さの問題でしたが、動いた様子をダイヤグラムに表してみると、意外と手掛かりはつかめるのではないかと思いました。
難易度はそれほど高くないはず。なので、合格のためには落とせない一題です。

以下は究学からのおすすめです。

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。