東大寺2015年度算数 大問1⑴

「東大寺学園算数入試問題を解いてみた」シリーズ。
教え子が東大寺学園を希望していて、久しぶりに本気で問題を解いています。
まずは大問1⑴。計算問題です。

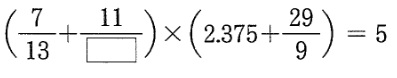
だいたい東大寺の計算問題は、問題の冒頭、しょっぱなにあります。
そしてたいてい激ムズ。並んでいる数字が難しいのですが、この年の問題はそれほどでもなさそうです。
2.375＝2\(\frac{3}{8}\)なので、最初の計算は
2.375＋\(\frac{29}{9}\)＝2\(\frac{3}{8}\)＋3\(\frac{2}{9}\)＝5\(\frac{43}{72}\)
次は、5÷5\(\frac{43}{72}\)＝5×\(\frac{72}{403}\)＝\(\frac{360}{403}\)
出てくる数字がだんだん嫌な感じになってきた…
次は、\(\frac{360}{403}\)－\(\frac{7}{13}\)＝\(\frac{360}{403}\)－\(\frac{217}{403}\)＝\(\frac{143}{403}\)　おっと、これは13で約分できる。
\(\frac{143}{403}\)＝\(\frac{11}{31}\)か。だから答えは31　

素直な問題でよかった・・・

以下は究学からのおすすめです。

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。