東大寺2019年度算数 大問3⑵

東大寺らしい、シンプルで面白い問題です。

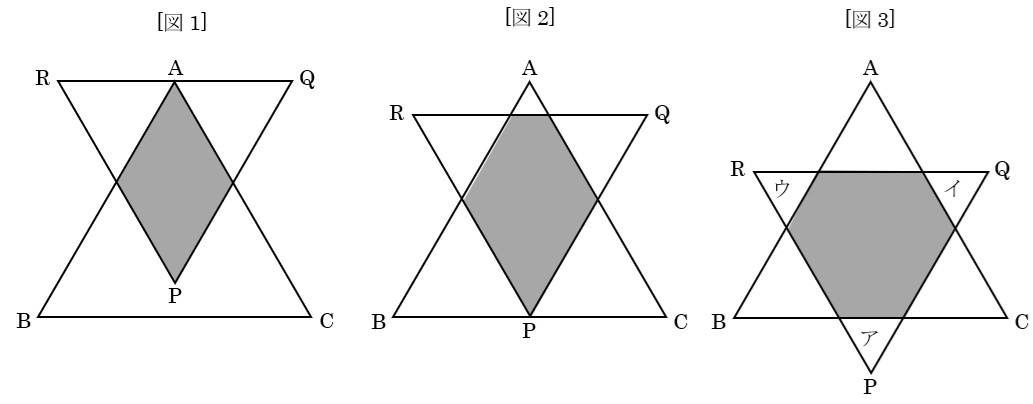
大小2個の正三角形ABCと正三角形PQRを下の3つの図のようにかさねました。
　[図1]　RQとBCが平行で，AがRQの真ん中の点と重なる。
　[図2]　RQとBCが平行で，PがBCの真ん中の点と重なる。
　[図3]　RQとBCが平行で，3つの正三角形ア，イ，ウがすべて合同になる。

それぞれの図において，正三角形ABCと正三角形PQRが重なっている部分（図の塗りつぶした部分）を考えます。[図1]において，正三角形ABCと正三角形PQRが重なっている部分の面積は10cm²で，[図2]において，正三角形ABCと正三角形PQRが重なっている部分の面積は14cm²でした。
①　正三角形PQRの面積を求めなさい。

図のように補助線DEを引くといい。

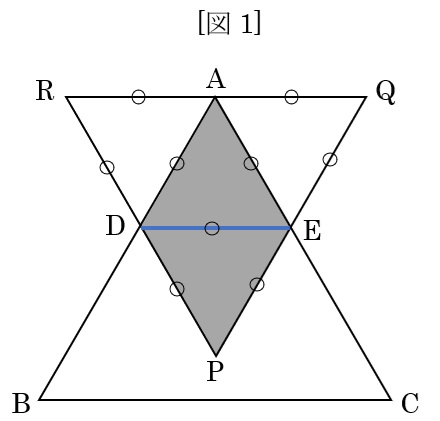
正三角形PQRが4つの合同な正三角形に分けられる。このうち2つ分の面積の合計が10cm2なので、正三角形PQRの面積は、10÷2×4＝20cm²　

②　[図3]において，正三角形ABCと正三角形PQRが重なっている部分の面積を求めなさい。

これはなかなか厄介な問題です。

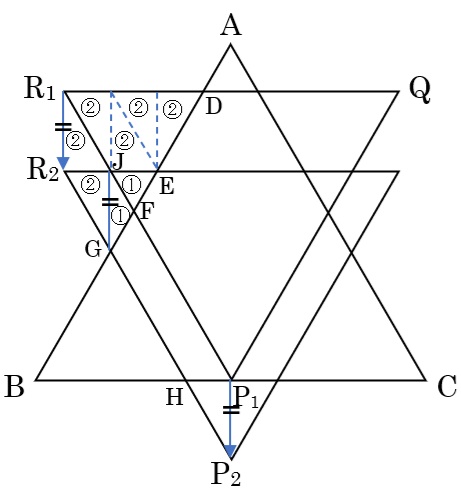
図2と図3を重ねて三角形PQRの動きを考えるといいでしょう。
図で、P₁P₂＝R₁R₂なので、三角形P₁P₂Hと三角形R₁R₂Jは合同で、どちらも[図3]のはみ出した正三角形の半分です。これは三角形R₂GFとも合同で、この面積を②としましょう。
すると、三角形EJF＝①となります。
また、四角形R₁JEDを図のように分割すると、三角形R₁FD＝⑨です。
三角形R₁FD＝(20－14)÷2＝3cm²なので、⑨＝3cm²より①＝\(\frac{1}{3}\)となり、[図3]のはみ出した正三角形1つ分の面積は④＝\(\frac{1}{3}\)×4＝\(\frac{4}{3}\)cm²
以上から、重なった部分の面積は、20－\(\frac{4}{3}\)×3＝16cm²となります。

それぞれの図をそれだけ見ていてもいい考えは浮かびません。
この場合、正三角形PQRを実際に動かすことで解決策への道筋が浮かぶでしょう。

以下は究学からのおすすめです。

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。