東大寺学園の2018年度算数入試問題の大問3⑵は、なかなか厄介だ。
図形のまわりを円が転がりながら進むときの、直線部分のみ考える問題。
通常は、180度より小さい角の外側を転がることを考えたらいいのだが、この問題では内側を考えないといけない。厄介だ。
正確な図で考える必要がありそうだ。
図形㋐,図形㋑,図形㋒は1辺の長さが10cmの正三角形をそれぞれ6個,4個,5個合わせてできた図形です。これらの3つの図形と,円Pがあります。円Pを図形㋐の周に沿って離れることなくその外側を一周させたとき,中心が動いてできる線のうちの直線部分の長さと,円Pを図形㋑の周に沿って離れることなくその外側を一周させたとき,中心が動いてできる線のうちの直線部分の長さとの差は1.5cmでした。円Pを図形㋑の周に沿って離れることなくその外側を一周させたとき,中心が動いてできる線のうちの直線部分の長さを求めなさい。
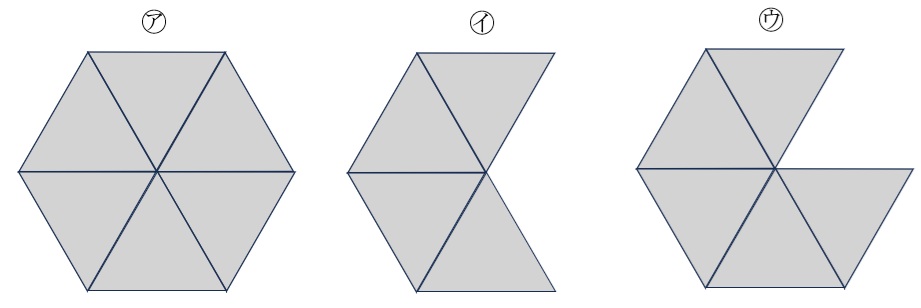
㋐の周囲を円が進むとき、直線部分の長さは10cm×6=60cm
㋑の周囲を円が進むとき、直線部分の長さは60-1.5=58.5cm
この部分を詳しく見てみよう。図の赤線部分AB2つ分が短くなった1.5cm
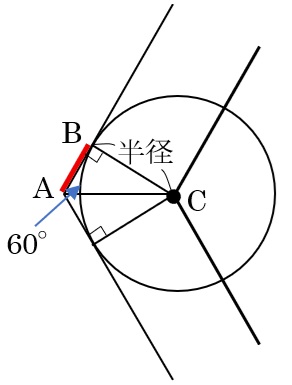
1.5÷2=0.75cm・・・AB
三角形ABCは30度・60度・90度の直角三角形。
㋒で円の中心が動く直線部分は下の図の三角形DEFのDE×2だけ短くなる。
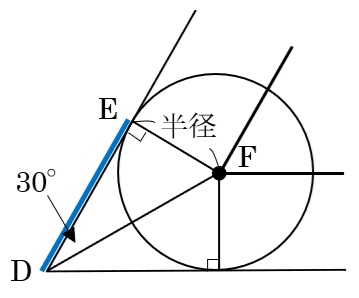
三角形DEFと三角形ABCの関係からDEの長さを考えましょう。
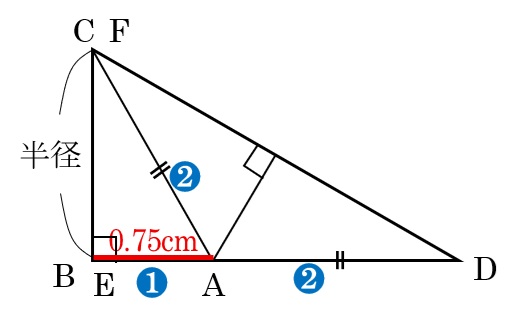
AC=AD=②,AB=①=0.75cmより、DE=2.25cm
㋒で直線部分の長さは、10×7-2.25×2=65.5cmとなる。
大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
算国オンライン個別指導塾究学の生徒も募集しています(年中いつでも歓迎します。まずは無料体験で)



