大問2は長いなが~い食塩水の問題。問題文がやたら長い。ここで心が折れそうになるのを鼓舞して、さぁ、解くか。
2種類の食塩水PとQがあり,食塩水Pの濃度は食塩水Qの濃度よりも8%高くなっています。次の問いに答えなさい。
⑴ 400gの食塩水Pと600gの食塩水Qを1つの空の容器に入れてよくかき混ぜると,できあがった食塩水の濃度は,食塩水Qの濃度よりも何%高くなっていますか。
ここはてんびんが楽でしょう。
図のようなてんびんの図を描いて考えます。
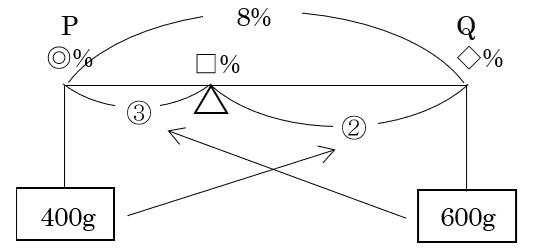
重さの比は400:600=2:3なので,支点からのうでの長さの比は3:2 → これを③,②とする
差の③+②=⑤が8%より②=8×\(\frac{2}{3+2}\)=3.2%
⑵ 空の容器Aに400gの食塩水Pを入れ,空の容器Bに600gの食塩水Qを入れました。それぞれの容器から120gずつの食塩水を取り出して,容器Aから取り出した食塩水を容器Bに入れ,容器Bから取り出した食塩水を容器Aに入れよくかき混ぜました。このとき,容器Aに入っている食塩水と容器Bに入っている食塩水の濃度の差は何%ですか。
等量交換の問題ですね。
Aの容器はPの食塩水が280g,Qの食塩水が120g,Bの容器はPの食塩水が120g,Qの食塩水が480g入ったことになります。それぞれの食塩水が混ざった様子をてんびんで表すといいですね。

左の図から、⑦=8%×\(\frac{7}{3+7}\)=5.6%
右の図から,1⃣=8%×\(\frac{1}{4+1}\)=1.6%
できあがった食塩水の濃度の差は,5.6-1.6=4%となります。
ここまでは、問題としてはふつうの難易度で,この程度の問題は確実に正解したいところです。
差がつくのは次の⑶ですかね。
⑶ 空の容器Aに400gの食塩水Pを入れ,空の容器Bに600gの食塩水Qを入れました。それぞれの容器から等しい重さの食塩水を取り出して,容器Aから取り出した食塩水を容器Bに入れ,容器Bから取り出した食塩水を容器Aに入れよくかき混ぜました。2つの容器の食塩水の濃度の差が2%になったとすると,それぞれの容器から取り出した食塩水の重さは何gずつでしたか。考えられるものをすべて答えなさい。
何gの入れかえか分からないので、てんびんだと苦しいかもしれません。
そこで、少しずつ入れかえる量を変化させていく方法を試してみましょう。
ア:30gの入れかえ
Aの容器は Qの濃度+8%×\(\frac{37}{40}\)=Qの濃度+7.4%
Bの容器は Qの濃度+8%×\(\frac{1}{20}\)=Qの濃度+0.4%
⇒7.4-0.4=7%の差
イ:60gの入れかえ
Aの容器は Qの濃度+8%×\(\frac{17}{20}\)=Qの濃度+6.8%
Bの容器は Qの濃度+8%×\(\frac{1}{10}\)=Qの濃度+0.8%
⇒6.8-0.8=6%の差
ウ:90gの入れかえ
Aの容器は Qの濃度+8%×\(\frac{31}{40}\)=Qの濃度+6.2%
Bの容器は Qの濃度+8%×\(\frac{3}{20}\)=Qの濃度+1.2%
⇒6.2-1.2=5%の差
このように30gずつ入れかえる量を変化させていくと、濃度の差が1%ずつ減っていくことが分かります。
120g→4%,150g→3%,そして180gで2%となります。
さらに変化させると、
210g→1%,240g→0%
さらに変化させていくと、今度は差が増えていきます。
270g→1%,300g→2%
以上から、差が2%になるのは180gと300g
大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
算国オンライン個別指導塾究学の生徒も募集しています(年中いつでも歓迎します。まずは無料体験で)



