
灘中学校の2021年度算数~2日目大問4
はじめ,3枚のカード1,2,3が左からこの順に並んでいます。これらのカードの並べ替えを何回かします。1回の並べ替えにつき,次の(A)~(D)のどれか1つが行われます。
(A)最も左にあるカードを右端に移動させる。
(B)最も右にあるカードを左端に移動させる。
(C)最も左にあるカードを残り2枚の間に移動させる。
(D)最も右にあるカードを残り2枚の間に移動させる。
例えば,1回目に(A),2回目に(C)の並べ替えをすると,カードの並びは
123 → 231 → 321
と変化します。
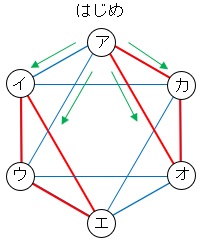
⑴ 右の図で,線でつながれた並びどうしは,(A)~(D)のいずれか1回の並べ替えで変わります。右の図の9つの空欄に1~3のいずれかの数字を入れなさい。
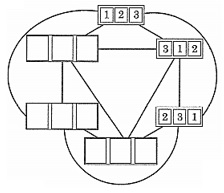
⑵ 3回の並べ替えで初めて123の並びに戻るような,3回の並べ替えの方法は全部で□通りあります。
⑶ 5回の並べ替えで初めて123の並びに戻るような,5回の並べ替えの方法は全部で□通りあります。
⑷ ⑶の並べ替えの方法のうち,(A)の並べ替えの回数と(B)の並べ替えの回数の合計が5回であるものは全部で□通りあります。
⑸ ⑶の並べ替えの方法のうち,(A)の並べ替えの回数と(B)の並べ替えの回数の合計が1回または3回であるものは全部で□通りあります。
➤➤➤解説
なかなか面白い場合の数の問題です。
⑴は実際に作業しながら数字を入れていきましょう。これはすぐにできますよね。
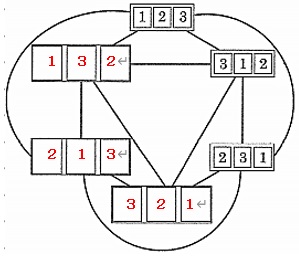
この作業をするときに、ついでにそれぞれの数字の並びをつなぐ線に、どれを使って変換したかも記入しましょう。
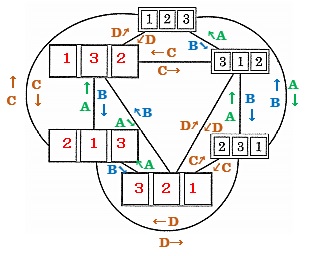
面白いことに気づきます。
Aの作業の反対はBで,Bの反対はAですが、C,Dの反対はそのまま同じC,Dになっているということ。
とりあえず、問題に戻りましょう。
⑵ 「3回の並べ替えで初めて123の並びに戻る」とあるので、この図をもっと見やすく書き直して考えましょう。
6種類の数字の並びを,123をア,132をイ,…として,赤線はAかBでの変換,青線はCかDでの変換を表します。表します。
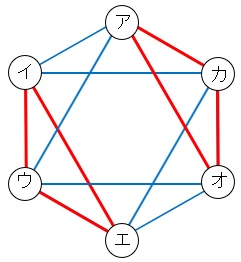
1回の変換で、線でつながったどこにでも行けるので、それぞれの記号の場所に行く行き方が「何回目に何通りあるか」を記入していきます(要するに「イチイチ解法」ですね)。
ただし、途中で123つまりアに行ってはいけないので、注意しましょう。
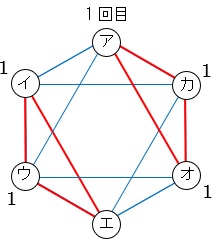
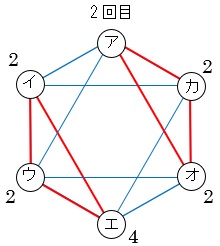
3回目にアにもどるのはイ,ウ,オ,カからなので、2+2+2+2=8通り。
⑶ 「5回の並べ替えで初めて123の並びに戻る」とあるので、先の図に続けて3回目、4回目の図も描きます。
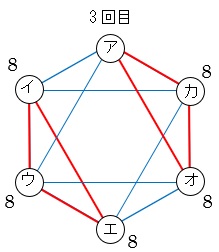
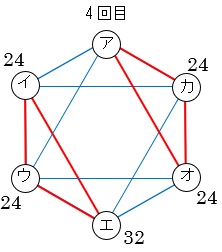
5回目にアにもどるのはイ,ウ,オ,カからなので、24+24+24+24=96通り。
⑷ 5回とも赤線を通っての変換なので、図のア,カ,オだけでイチイチ解法します。
何回目やっても,オもカも1にしかなりませんから、1+1=2通り。
⑸ 5回の変換でアにもどるとき、
・青線だけを通過するのは無理
・赤線を2回,4回通過してアに戻るのも無理
したがって、96-2=94通り
以上です。
——————–
それにしても、しっかりと図を通じてヒントを書いてくれていましたね。
この問題の難しいところは、イチイチ解法が使えることに気づくかどうか。
最初の段階で、漫然と図の中に数字を入れるだけだと、なかなか気づきづらいところです。
ある程度先を見越して、せっかく与えられた図を十分利用できたかどうかで合否が分かれそうな問題でした。
感動の30分を無料で体験
~スカイプ個別指導
➤ 今すぐ成績を上げたい
➤ 苦手な単元を攻略したい
➤ 志望校合格まであと一歩
➤ 志望校をあきらめたくない
以上のような受験生の皆さん、保護者の皆さん、今すぐ無料体験に申し込みましょう。
「感動の30分間」をぜひご自身で味わってください。