
Contents
灘中学校2021年度算数~1日目大問11
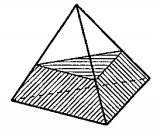
右の図のように,三角すいの形をした容器があり,4つの面の面積は16㎠,18㎠,20㎠,24㎠です。この容器にはいくらかの水が入っています。この容器を,4つの面のいずれかが水平な地面につくように置きます。容器の内側の面のうち水にぬれる部分の面積が最も大きくなるように置いたとき,水にぬれる部分の面積は60㎠になります。水にぬれる部分の面積が最も小さくなるように置いたとき,水にぬれる部分の面積は□㎠になります。
➤➤➤解説
この問題を考えるときのポイントは、「空気」に注目することです。
どの面を下に置いたとしても「空気の部分の三角すいは合同」です。
三角すいを側面から見たときのイメージ図をかいてみます。
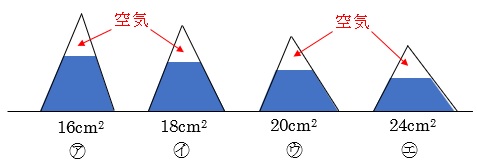
図の㋐~㋓の空気の部分の三角すいの側面積が最小になったとき(A)この容器の水にぬれる面積は最大になり、空気の部分の三角すいの側面積が最大になったとき(B)この容器の水にぬれる面積は最小になります。
(A)は24㎠を底面にした場合(図の㋓)で、(B)は16㎠を底面にした場合(図の㋐)ということはすぐに分かります。
㋓で空気の部分の側面積は16+18+20+24-60=18㎠
㋓の容器の側面積の合計は16+18+20=54㎠
容器の側面積と空気の三角すいの側面積の比は54:18=3:1
容器と空気の三角すいは相似なので、これはこの2つの「相似な」三角すいの対応する面積の比が3:1ということです。
㋐で、この3:1を利用しましょう。
㋐の容器の側面積は18+20+24=62㎠
㋐の空気の三角すいの側面積は62×$\frac{1}{3}$=20$\frac{2}{3}$㎠
ようやく答えに行きつきました。
この場合の水にぬれる部分の面積は
16+18+20+24-20$\frac{2}{3}$=57$\frac{1}{3}$㎠
難しい問題ですが、でも最難関受験生にはできてほしい
水に触れない部分、つまり空気が入っている部分の三角すいは、どの面を底面にした場合でも必ず合同になる。
これは、ふだん漫然と問題を解いているだけでは気づきにくいポイントです。
ですが、ふだんから空気の部分にも意識を向けてやっている受験生には「当然のこと」と受け止められるはず。
そして、灘中(だけでなく、関西の最難関中すべてにあてはまりますが)合格レベルの人には、この考え方は十分使えるはず。逆に言えば、ここまで達していない人は、最難関中学を受験してはいけません、的な問題でしょう。
感動の30分を無料で体験
~スカイプ個別指導
➤ 今すぐ成績を上げたい
➤ 苦手な単元を攻略したい
➤ 志望校合格まであと一歩
➤ 志望校をあきらめたくない
以上のような受験生の皆さん、保護者の皆さん、今すぐ無料体験に申し込みましょう。
「感動の30分間」をぜひご自身で味わってください。