東大寺2024年度算数 大問4

「東大寺の算数を解いてみた」シリーズ。
2024年度大問4の速さ（点の移動）の問題です。
非常にシンプルながら、奥が深い、ある意味とても東大寺らしい問題です。もちろん、簡単ではありませんよ。

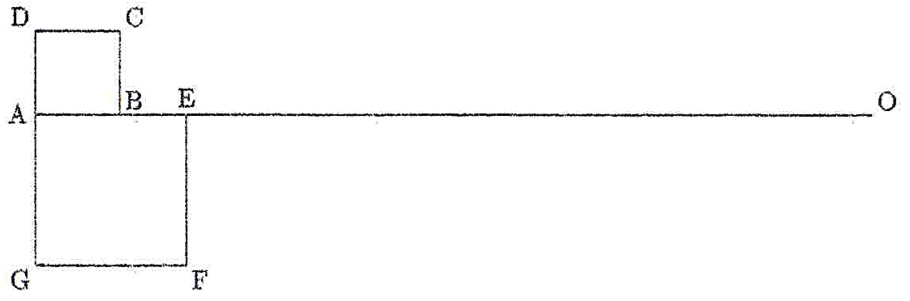
下の図のような，大きさの異なる正方形ABCD，正方形AEFGと直線AOを組み合わせた図形があります。この図形において，4つの点P，Q，R，Sを，Aを出発点として次に示すコース上をそれぞれ動かします。
　P，Rのコース…正方形ABCDの周を A → B → C → D → A の順に移動して一周し，
　　　　　　　　その後Oへ向かってまっすぐ移動する。
　Q，Sのコース…正方形AEFGの周を A → E → F → G → A の順に移動して一周し，
　　　　　　　　その後Oへ向かってまっすぐ移動する。
　ただし，OはEから遠いところにあり，P，Q，R，SがOに着くことは考えないものとします。

　まず，PとQをそれぞれ一定の速さで，Pが1分間に動く距離とQが1分間に動く距離の和が12cmとなるように動かします。すると，PとQが同時にAを出発してからちょうど10分後に，Pは正方形ABCDを一周したのちにEの位置にあり，Qは正方形AEFGを一周したのちにBの位置にありました。
⑴　DGの長さを求めなさい。

小さい正方形の1辺の長さを①，大きい正方形の1辺の長さを1⃣としましょう。
Pが10分間で進むのは、④と1⃣　…　㋐
Qが10分間で進むのは、4⃣と①　…　㋑
㋐と㋑を合わせると、PとQが10分間で進んだのは⑤と5⃣で、この長さの合計は12×10＝120cmです。（⑤＋5⃣＝120）
DGの長さは①＋1⃣なので、120÷5＝24cmになります。

⑵　PとQがA以外の点で重なるのはAを出発してから何分何秒後ですか。また，この重なる位置の点をKとするとき，AKの長さを求めなさい。

10分後、PはEに、QはBにある。
⑴と同様に、小さい正方形の1辺を①、大きい正方形の1辺を1⃣として、少し工夫した図で表してみることにした。

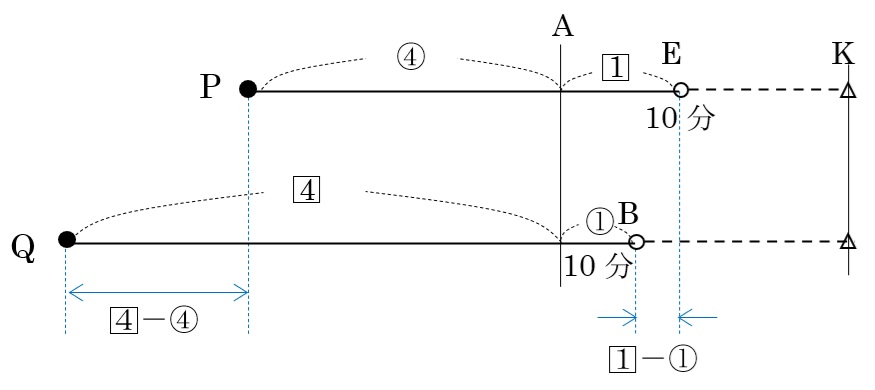
Pは④進んで再びAに、Qは4⃣進んで再びAに戻る。
PがEにきたとき、QはBにいて、図から分かるようにその差は1⃣－①
この「1⃣－①」を追いつくのにかかる時間を考える。
出発したときPとQのいる場所には「4⃣－④」の差で、これが10分で「1⃣－①」になったので、
Qは10分で、(4⃣－④)－(1⃣－①)＝3⃣－③追いついた。
だから、1⃣－①を追いつく時間は、10分÷3＝3\(\frac{1}{3}\)分＝3分20秒
ということで、これは出発してから13分20秒後ということになる。

次に、AKの長さ。
13分20秒で、PとQが進んだ距離の合計は、12×13\(\frac{1}{3}\)＝160cm
ここから④＋4⃣を引けば、AK2つ分が残る。
⑴より、①＋1⃣＝24cmなので、160－24×4＝64cm　…AK2つ分
AKの長さは64÷2＝32cmですね。

次に，RとSをそれぞれ一定の速さで動かします。RとSが同時にAを出発してからちょうど12分後に，RとSは⑵の点Kより6cmだけOの方向に進んだ点で重なりました。
⑶　RとSが重なる3分前のRの位置の点をLとします。ELの長さを求めなさい。

SがRと重なる点をMとしましょう。
AMの長さは、32＋6＝38cm
Rは12分間で④＋38cmを進んだことになります。
3分は12分の\(\frac{1}{4}\)なので、LはMから、(④＋38cm)÷4＝①＋9.5cmはなれたところにあります。（下の図参照）

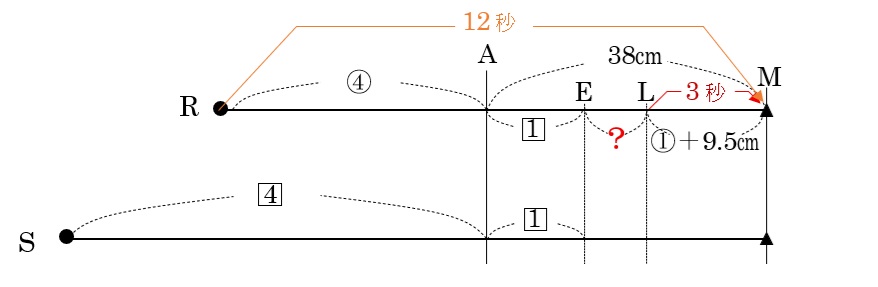
1⃣＋①＝24cmでしたから、EL（図の？の部分）の長さは
38cm－(1⃣＋①＋9.5cm)＝38cm－(24cm＋9.5cm)＝4.5cmですね。

究学からのご案内

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。

➪2024年度大阪星光算数入試問題と解説、見本を無料進呈しています。