東大寺2024年度算数 大問1

「東大寺の算数を解いてみた」シリーズ。
今回は2024年度（令和6年度）の問題です。
まずは大問1からで、円周率は3.14を使え、だとか、円すいや角すいの体積の求め方が注意書きに書いてある。

１　次の各問いに答えなさい。（解答欄には答えのみを記入しなさい。）
⑴　0.775×7.5＋5.5÷\(\frac{4}{7}\)＋15.75÷2.4

全部小数で求められるので、小数でやってみましょう。
・0.775×7.5＝5.8125
・5.5÷\(\frac{4}{7}\)＝5.5×7÷4＝9.625
・15.75÷2.4＝6.5625
よって、5.8125＋9.625＋6.5625＝22でこれが答えです。
もちろん、分数でも求められますね。
・0.775×7.5＝\(\frac{775}{1000}\)×\(\frac{75}{10}\)＝\(\frac{31}{40}\)×\(\frac{15}{2}\)＝\(\frac{93}{16}\)
・5.5÷\(\frac{4}{7}\)＝\(\frac{11}{2}\)×\(\frac{7}{4}\)＝\(\frac{77}{8}\)
・15.75÷2.4＝\(\frac{63}{4}\)÷\(\frac{12}{5}\)＝\(\frac{63}{4}\)×\(\frac{5}{12}\)＝\(\frac{105}{16}\)
よって、\(\frac{93}{16}\)＋\(\frac{154}{16}\)＋\(\frac{105}{16}\)＝\(\frac{352}{16}\)＝22となります。
どちらもそれなりに面倒くさい・・・

⑵　次の空欄に適切な数を入れて正しい式にしなさい。
105×{(2024＋□)×\(\frac{1}{4}\)×\(\frac{1}{5}\)×\(\frac{1}{6}\)×\(\frac{1}{7}\)×\(\frac{1}{8}\)＋\(\frac{2}{15}\)}＝78

いやぁ、これもなかなか難儀そうな問題ですやん。
とりあえず、ここから。
(2024＋□)×\(\frac{1}{4}\)×\(\frac{1}{5}\)×\(\frac{1}{6}\)×\(\frac{1}{7}\)×\(\frac{1}{8}\)＋\(\frac{2}{15}\)＝78÷105＝\(\frac{26}{35}\)
\(\frac{26}{35}\)－\(\frac{2}{15}\)＝\(\frac{78－14}{105}\)＝\(\frac{64}{105}\)
なので、2024＋□＝\(\frac{64}{105}\)×8×7×6×5×4＝64×8×2×4＝4096
で、□＝4096－2024＝2072だ。
最後、約分もしっかりできたし、ボク的には⑴よりましかな？

⑶　45との最大公約数が1となるような1以上の整数のうち，小さい方から345番目の数を求めなさい。

まずは45を素因数分解、っと…
45＝3×3×5
ということは、3の倍数でも5の倍数でもない数を小さい順に考えて345番目、ということでいい気がする。
さて、3と5の最小公倍数は15なので、1～15で該当する数を書き出せば、
1，2，4，7，8，11，13，14の8個　　　　　　　　←これを1セット目としましょう
次の16～30にも、それぞれ15増えた数が8個　　　　←これは2セット目
次の31～45にも、それぞれさらに15増えた数が8個　←これは3セット目
・・・
というわけで、計算でできそうですね。（まさか書き出しではしないでしょ？）
345÷8＝43余り1なので、44セット目の最初の数っぽい。
1＋15×43＝646となりますね。

⑷　下の図で，ABとPQはどちらもBDと垂直です。三角形ACDをPQのまわりに1回転させたときにできる立体の体積を求めなさい。

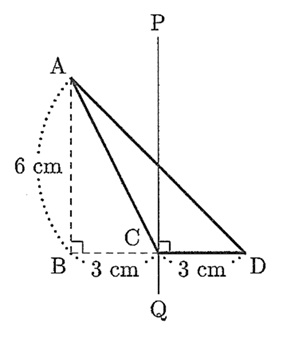
「㋐底面の半径が3cmで高さ2cmの円すい台＋㋑底面の半径が3cmで高さ4cmの円すい台－㋒底面の半径が3cmで高さ3cmの円すい」で求めましょう。

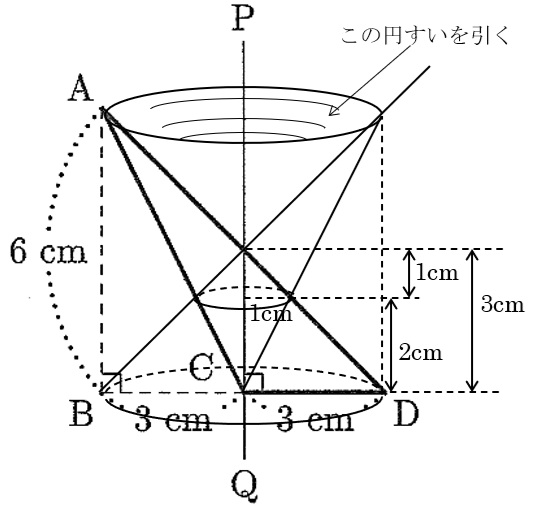
㋐は”底面の半径が3cmで高さ3cmの円すい－底面の半径が1cmで高さ1cmの円すい”で求めてもいいし、またはこの2つの体積比が27：1であることを考えて
底面の半径が3cmで高さ3cmの円すい×\(\frac{26}{27}\)で求めてもいいな。
㋑も同様に、”底面の半径が3cmで高さ6cmの円すい－底面の半径が1cmで高さ2cmの円すい”で求めてもいいし、またはこの2つの体積比が27：1であることを考えて
底面の半径が3cmで高さ6cmの円すい×\(\frac{26}{27}\)で求めてもいい。
さて、式を作って計算しようぜ。
3×3×π×3×\(\frac{1}{3}\)×\(\frac{26}{27}\)＋3×3×π×6×\(\frac{1}{3}\)×\(\frac{26}{27}\)－3×3×π×3×\(\frac{1}{3}\)＝\(\frac{26}{3}\)×π＋\(\frac{52}{3}\)×π－9×π＝17×π＝53.38cm³となる。

究学からのご案内

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。

➪2024年度大阪星光算数入試問題と解説、見本を無料進呈しています。