東大寺2014年度算数 大問1⑵

「東大寺の算数を解いてみた」シリーズ。
2014年度大問1⑵、平面図形の問題です。

右の図の四角形ABCDは1辺の長さが12cmの正方形で，Pはその内部の点です。
　三角形ABPの面積：三角形DAPの面積＝3：4，
　三角形BCPの面積：三角形CDPの面積＝1：3
のとき，三角形ABPの面積を求めなさい。

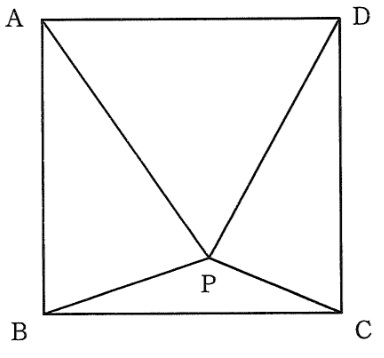
下の図のように、三角形ABPの面積＝③，三角形DAPの面積＝④，
三角形BCPの面積＝1⃣，三角形CDPの面積＝3⃣
とする。

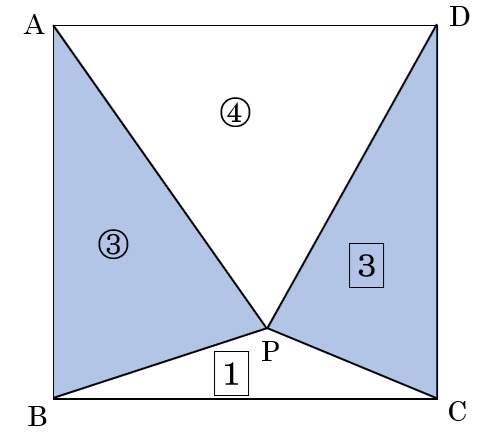
色をつけた部分の２つの三角形ABPと三角形CDPの面積の和は正方形の面積の半分
三角形ADPの面積と三角形CDPの面積の和も正方形の面積の半分
つまり、③＋3⃣＝④＋1⃣となります。
ここから、2⃣＝①となるので、③＝6⃣、④＝8⃣
よって、三角形ABPの面積は、12×12×\(\frac{6}{8＋6＋1＋3}\)＝12×12×\(\frac{1}{3}\)＝48cm²となります。

※　消去算で求めてもいいですね。
正方形の面積の半分は72cm²なので、
　③＋3⃣＝72　→　③＋3⃣＝72
　④＋1⃣＝72　→　⑫＋3⃣＝216
ここから⑨＝216－72＝144cm²
三角形ABP＝144×\(\frac{3}{9}\)＝48cm²　

東大寺の合格を真剣に考えるなら、この問題は「秒で解ける」ぐらいの勢いでやってください。

究学からご案内

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。