東大寺2022年度算数 大問1⑵

「東大寺の算数を解いてみた」シリーズ。
2022年度の問題です。今回は、大問1⑵で、点の移動とそれに伴う図形を考える問題。
ではさっそく、解いてみましょう。

図の長方形ABCDは紙でできていて，対角線の長さはABの長さの2倍です。点PはAD上をAからDまで動きます。三角形ABPをBPを折り目として折り返したとき，紙が2枚重なっている部分の面積をSとします。

(ⅰ)　Pが点Eに一致するまでは，SはAPの長さに比例し，Eを通り過ぎると，SはAPの長さに比例しなくなります。このEに対し，∠ABEの大きさを求めなさい。ただし，たとえば三角形XYZについて，頂点Yでの内角を∠XYZまたは∠ZYXと表します。

頂点Aが移動した点をGとしましょう。
PA＝PGです。重なった直角三角形の底辺をBG，高さをPGとします。
Pの移動に伴い、高さPGは増えていきますが底辺BGは一定なので、「SはAPの長さに比例」します。

ところがPが点Eを超えると、重なった部分が三角形ABPと同じ形ではなくなります。

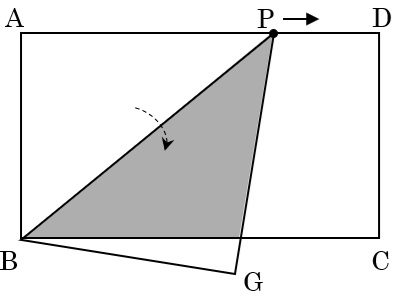
三角形ABPが重なった部分Sと完全に同じになるのは、GがBC上にくるまで。

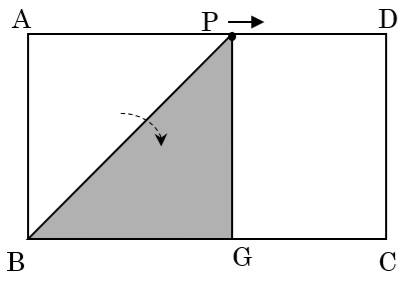
このとき、三角形ABPも三角形BGPも直角二等辺三角形になっています。（四角形ABGEが正方形になったとき）
よって、∠ABEは45度です。

(ⅱ)　Pが点Fに一致するときのSが，PがDに一致するときのSの\(\frac{1}{2}\)となります。このFに対し，AF：ADを最も簡単な整数の比で答えなさい。

この問題を考えるためには、PがDに一致したときの図をできるだけ正確に描くことが大切でしょう。
こととき、問題文の中の条件「対角線の長さはABの長さの2倍」に注意します。（三角形ABDは3つの角が30°，60°，90°の直角三角形）

このとき重なった部分は二等辺三角形になっています。
Pが点Fに一致するときのSはこの二等辺三角形の面積の\(\frac{1}{2}\)なので、次のような図が考えられます。

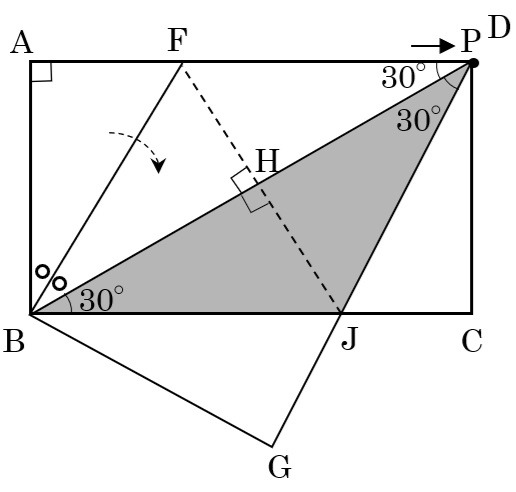
図の○印の角度は30度で、三角形BDFはFB＝FDの二等辺三角形
AF：FB＝1：2なので、AF：FD＝1：2
ですから、AF：AD＝1：3になります。

以下は究学からのおすすめです。

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。