2026年度 甲陽学院中学校(1日目)算数:難易度速報&分析
2026年度入試もほぼ終了し、様々な結果が出ている時期かと思います。受験生のみなさん、本当にお疲れ様でした。 問題が入手できた学校から順次解いていますが、今回は甲陽学院中学校(1日目)の算数を振り返ります。
結論から言うと、「難易度は例年通り〜やや易化。甲陽らしさは健在だが、前半の取りこぼしが命取りになる内容」でした。
「ま、それなりの難易度。甲陽らしさ(?)はやや薄く感じた。」というところです。
以下、ボクなりの難易度分析ととっておきたいレベルも記載しておきます。
難易度分析はA(甲陽にしては簡単)、B(甲陽にしては普通)、C(難しい)
とっておきたいレベルは、◎(ぜひ正解を)、○(できれば正解したい)、△(できたら差をつけられる)、■(できなくてよい)
■ 2026年度 難易度・目標レベル一覧
まずは全体の構成と、ボクの多少偏見があるかもしれない分析による優先順位をまとめました。
| 大問 | 分野 | 難易度 | 目標 | 備考 |
| 1 | 計算・立体切断 | A | ◎ | 完答必須。ここでリズムを作りたい |
| 2 | ニュートン算 | A | ◎ | 典型題。計算ミスに注意 |
| 3 | 平面図形と比 | B | ○〜△ | ⑵の相似の連鎖に気づけるか |
| 4 | 流水算 | B | ○〜△ | ダイヤグラムで視覚化すれば素直 |
| 5 | 変則時計算 | B | △ | 【甲陽らしい】 丁寧な状況把握が必要 |
| 6 | 規則性 | C | △〜■ | ⑶は「ある性質」に気づけば瞬殺だが… |
大問1 計算と立体切断
大問1の⑴は計算問題。落ち着いて解けば問題ないレベル。
大問1の⑵は直方体の斜め切断についての問題で、これも高さの平均の半分を求めるだけ。なんか簡単やな…
⑴ A、◎ ⑵ A、◎
大問2はニュートン算
大問2はニュートン算。別にギミックもなく、素直に今まで習った通り解けば、⑴⑵⑶すべて正解が得られる。少し計算が面倒ではありますが、きちんと解いて得点しておきたい。
⑴ A、◎ ⑵ A、◎
大問3 平面図形と比
大問3は図形の問題です。出題された図形は以下の通り。
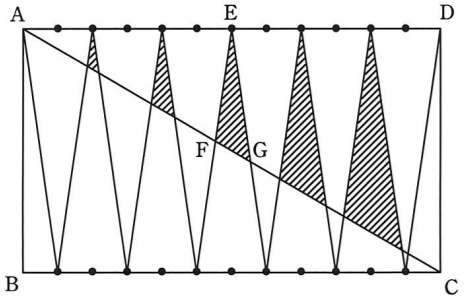
今までやってきた図形問題からかけ離れてもおらず、相似を利用して素直に比が求められたら十分得点できますね。
⑴は三角形EFGと長方形ABCDの面積の比較。
解き方はいろいろ思いつくけど、AE:ADとかAG:GCとか、AF:FCとかの比が分かると簡単。
で、⑵は斜線がついたすべての三角形の面積の和と長方形ABCDの面積の比を求める問題。
斜線がついた5つの三角形はすべて相似だと気づいたかな?
その上で、辺の比が1:2:3:4:5のなっていることを利用すると、⑴の結果を使って面積の割合は簡単に求められる。
これはやや甲陽らしさを感じる問題でした。
⑴ A、○ ⑵ B、△
大問4は見たことありそうな流水算の問題
大問4は流水算。
ちょっと難問の掲載された入試用の問題集あたりで見かけそうな問題。
見かけの通り、変な引っかけもなく、素直に解ける問題だな。
ボクはダイヤグラムをかいてやりました。
難易度も甲陽にしてはごくごく普通、というか易しめ。
⑴ A、◎ ⑵ A、〇 ⑶ B、△
大問5は変則時計の問題
次が非常に甲陽らしさを感じた問題です。
変則的な動きをする時計を使った時計算。
激ムズとまではいかないけど、時計の針の進む速さを、場所ごとに考えないといけないのでやや面倒。

12時から11時までは1時間に短針が27度ずつ進み、最後の1時間は63度進む、長針もこの目盛りに合わせた速さになる。
⑴では、それぞれの針の各区間での速さを求めることになっている。
⑵⑶は⑴で求めた速さを利用して解けばいい。
計算は少しだけやっかいだけど、仕組みが分かると正解できそうな問題。
以下、問題の意味を十分読み取ったうえで、という前提です。
⑴ B、〇 ⑵ B、△ ⑶ B、△
最後の大問6は規則性の問題。これは実際の問題を見てもらおうかな。

体裁は少しいじりましたが、実際の問題を「ほぼ」そのまま掲載しました。
⑴⑵はあまり何も考えずとも、書かれた条件から答えに行きつくのはそう手間ではありません。
⑴はそのまま当てはめればいいし、⑵は「逆」にたどっていくだけ。回数を増やすために「1引いて2倍する」ことを繰り返していけばいいのです。(すぐに気づくと思います。)
だけど、⑶は条件に合うものを「すべて」求める必要があって、いちいち書き出していたら結構時間がかかり、しかも途中で1つでもミスをしてしまったら即終了。
実はこの問題、受験生ならだれでも知っている「あること」を使えると気づいたらとても簡単に解けてしまいます。
この「あること」に気付けるかどうか、は1からいくつか遡って作業してみることも必要。⑵を解いたとき、そのヒントぐらいには気づいているかもしれません。
遡って順番に何通りあるか調べていったら、その数の並びが「ある数列に」なっています。
そのうちこのブログで詳しく解説しますので、そちらをお待ちくださいね。
■ 来年度に向けた「甲陽対策の教訓」
今年の入試を解いて感じた、新6年生へのアドバイスは2点です。
- 「典型題での失点」は致命傷になる 大問1〜4のような標準レベルの問題を、確実に、かつ短時間で仕留める「基礎体力」が必須です。B問題レベルを「なんとなく」ではなく「完璧に」仕上げましょう。
- 「初見のルール」を面白がる粘り強さ 大問5や6のような独自のルール設定に対し、パニックにならずに条件を読み取る力。日頃から初見の問題に対し、調べたり試行錯誤したりする訓練を積んでおきましょう。
今回の1日目の目標は「7割(70点)」。 基礎を固め、粘り強く条件を整理できれば、十分に届く数字です。
【お知らせ:算国オンライン個別指導塾「究学」】
「解き方」を覚える子から、「考え方」を創る子へ。
今回の甲陽の問題のように、初見の条件を紐解く力は「本質的な思考の土台」があってこそ発揮されます。究学では、算数と国語の「なぜ?」を大切にし、中学受験のその先まで伸び続ける知性を育てます。



