東大寺2015年度算数 大問5

「東大寺の算数を解いてみた」シリーズ。
今回は2015年度の大問5、最後の問題です。
これも一見難しそうではありますが、いやいや、よく考えると…

図のようなAB＝20cm，BC=10cm，CG＝12cmの，面ADHEだけが空いている直方体の容器ABCDEFGHが水平な床の上に置いてあります。PQ=16cm，QR=12cm，RS＝18cmでPQとSRが平行である台形PQRSの板を図のように，Qが辺BCの真ん中に，Rが辺FGの真ん中にくるように，容器の底BCGFにまっすぐに立て，この容器いっぱいに水を満たしました。辺BFを床につけたまま，この容器を矢印の方向にゆっくりと45°傾けて水を流し出して，また底BCGFが床にピッタリついたもとの状態にゆっくりともどしました。ただし，板PQRSと容器はすきまなくくっついているものとし，板PQRSと容器の厚みは考えないものとします。

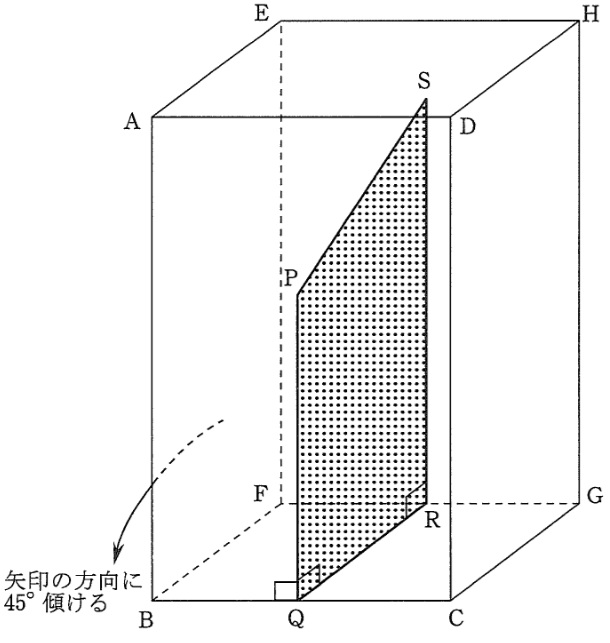
⑴　何cm³の水が流れ出たか求めなさい。

仕切り板は台形の形をしています。当然水はその板の一番低いところから流れ出しますから、仕切り板を高さがPQ＝16cmと考えて解きましょう。
容器を45度傾けたようすを、面ABCD側から見た図で考えるといいでしょう。

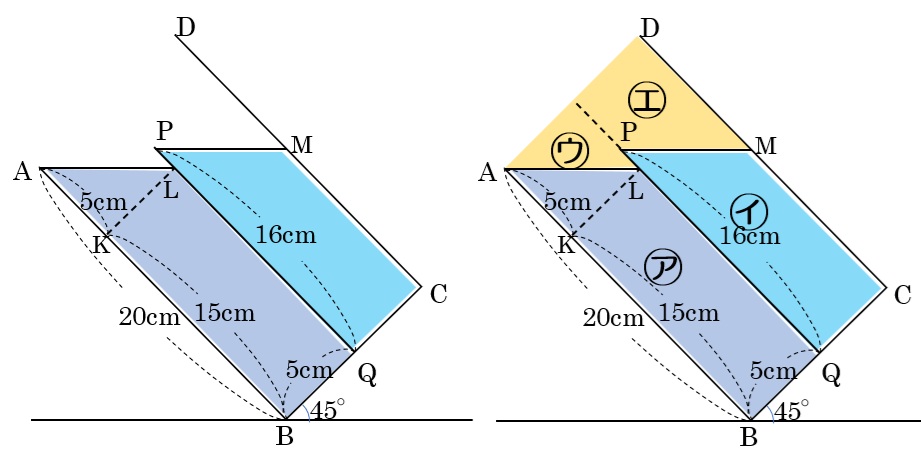
上の図左が45度傾けたときの水の様子です。
仕切り板の右側の水が、仕切り板でせき止められている感じです。
流れ出た水は、右側の図で㋒，㋓と書いた部分です、
㋒の面積は5×5÷2＝125cm²なので、体積は12.5×12＝150cm³
㋓の面積はMC＝16－5＝11cmなのでDM＝9cmより
(4＋9)×5÷2＝32.5cm²となり、体積は32.5×12＝390cm³　
よって流れ出た水は、150＋390＝540cm³です。

⑵　残った水は板PQRSによって2つの部分に分けられますが，頂点Cと同じ側に入っている水の水面の高さを求めなさい。

仕切りの左側にはPの高さまでしか水が入りません。流れた後の残りの水のうち仕切りの左側に入った水を除いた水が仕切りの右側にあることになります。
仕切りの左側の水量：5×12×16＝960cm³　
流れ出た後の水量：10×12×20－540＝1860cm³　
仕切りの右側の水量：1860－960＝900cm³　
深さは900÷(5×12)＝15cm

仕切り板が台形をしていることで戸惑う人も多いのではないかと思いますが、水は一番低いところから流れ出すので、それを意識して解くと意外と解けるものです。

以下は究学からのおすすめです。

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。