東大寺2015年度算数 大問3⑵

「東大寺の算数を解いてみた」シリーズ。
今回は2015年度の大問3⑵です。
2点が長方形の周囲を移動する問題ですが、図さえかけたら楽勝！のはずなんだけど・・・

図のような長方形ABCDがあります。点Pは頂点Aを出発して，長方形の周上を時計回りと逆向きでA → B → C → D → A の順に，点Qは頂点Aを出発して，長方形の周上を時計回りでA → D → C → B → A の順に，それぞれ一定の速さで一周するものとします。2点P，Qが同時に頂点Aを出発してから5.2秒後に，点Pは辺BC上に，点Qは辺DC上にあり，三角形APQが直角二等辺三角形になりました。2点P，Qが重なるのはそれから何秒後ですか。

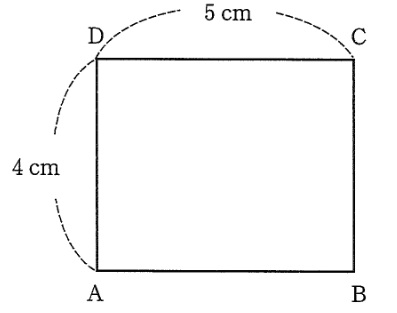
まずは、三角形APQが直角二等辺三角形になった（このとき、点PはBC上、点QはDC上）とあるので、その図を描くことから始めます。

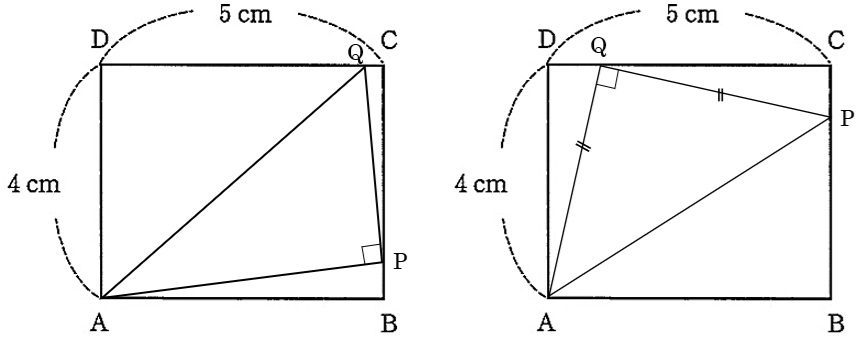
直角二等辺三角形APQで、角Aが直角になることはできないので、直角になるのは角Pか角Qのどちらかです。
上の図より、角Pが直角になるように描いてみてもPAとPQは等しくなりません。
角Qが直角になるように描けば、QA＝QPの直角二等辺三角形ができます。
このとき、三角形ADQと三角形QCPは合同になり、
AD＝QC＝4cm、DQ＝CP＝1cmと分かります。

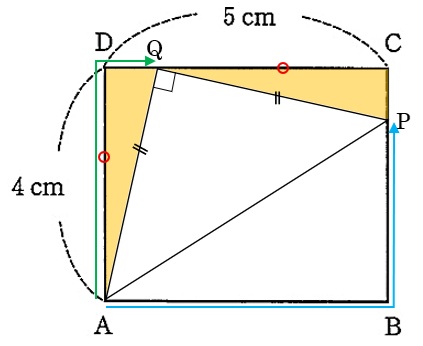
5.2秒で点Pは5＋(4－1)＝8cm、点Qは4＋1＝5cm進んだとわかるので、今からPとQが出会うまでの時間は、(4＋1)÷(\(\frac{8}{5.2}\)＋\(\frac{5}{5.2}\))＝2秒後と分かります。

図さえかけたら簡単な問題でした。合格のためには、落としてはいけない問題ですね。

以下は究学からのおすすめです。

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。