東大寺2025年度算数 大問3

「東大寺の算数を解いてみた」シリーズ。
今回は、2025年度入試問題から大問3の立体図形の問題です。
切断という、苦手な子は苦手な問題ですよ。
では早速取り組んでみましょう。

下の図のように，一辺の長さが4cmの立方体ABCD-EFGHがあり，辺AD，BC，FG上にそれぞれ点I，J，Kがあります。AI，CJ，FKの長さがどれも1cmであるとき，この立方体を次の平面で切ったときにできる立体のうち，点Bを含むものの体積を求めなさい。

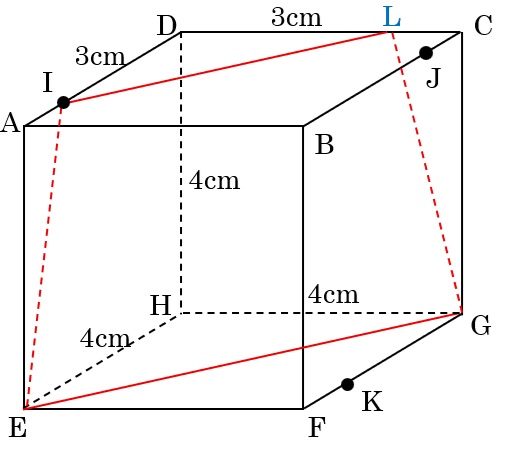
⑴　3点E，G，Iを通る平面

切り口の線は図のようになる。

EI，GJ，HDを延長したら点Mで交わる。

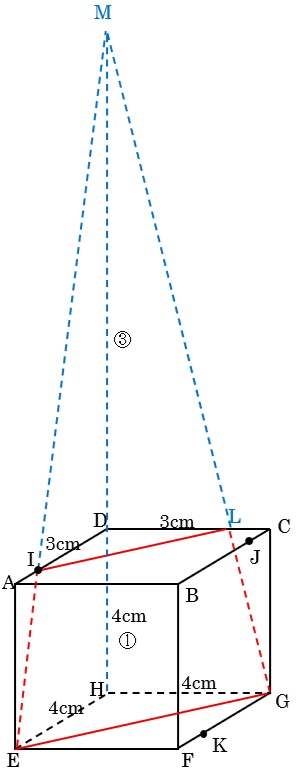
三角すい台DIL-HEGの体積は、三角すいM-HEGから三角すいM-DILを引いて求めることができる。
三角すいM-HEG　…　4×4÷2×16÷3＝\(\frac{128}{3}\)cm³
三角すいM-DIL　…　3×3÷2×12÷3＝18cm³
三角すい台DIL-HEGの体積は、\(\frac{128}{3}\)－18＝\(\frac{74}{3}\)＝24\(\frac{2}{3}\)なので、
Bを含む立体の体積は、4×4×4－24\(\frac{2}{3}\)＝39\(\frac{1}{3}\)cm³

⑵　3点E，K，Jを通る平面

切断面は下の図のようになる。
（この立方体を真上から見た図を参考にしてください。EKとNJが平行だから、長さを考えやすくなります。）

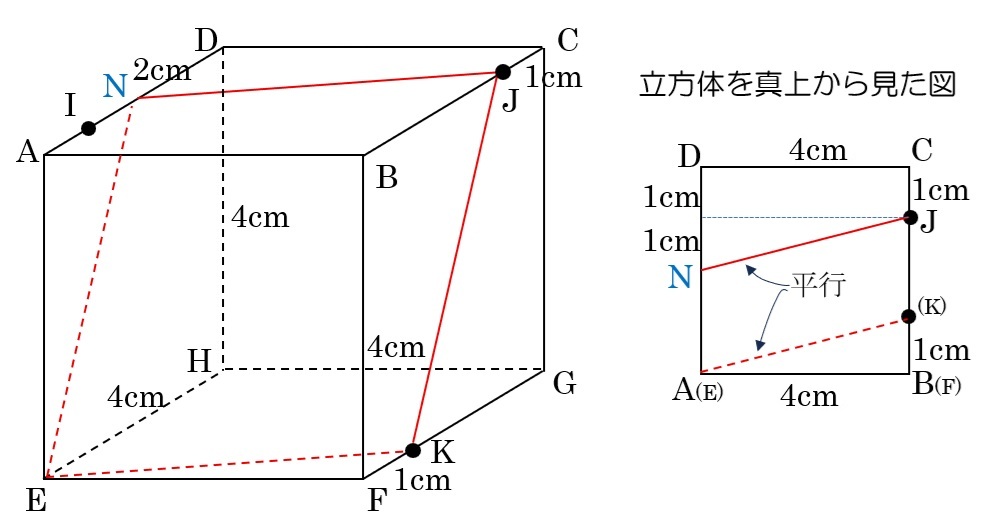
Bを含む方の立体は、底面をABCDとした四角柱を斜めに切断した立体です。

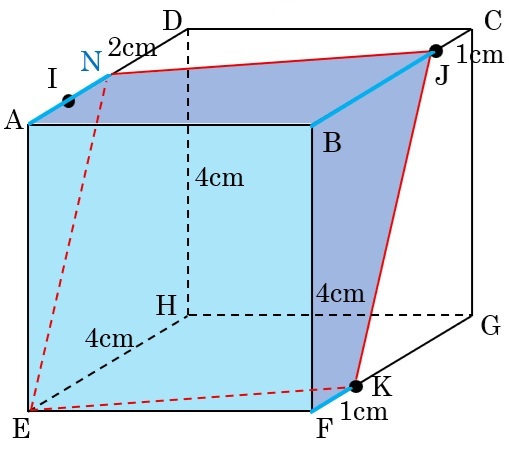
体積は「底面積×高さの平均」なので、4×4×\(\frac{0＋1＋3＋2}{4}\)＝24cm³となります。

⑶　3点E，G，Iを通る平面と3点E，K，Jを通る平面

⑴と⑵で切断した面で2回切断します。
こういった場合、注目するのは、2つの面の交わる部分です。平面と平面が交われば、交わった部分が直線になるので、それを手掛かりに考えていきましょう。

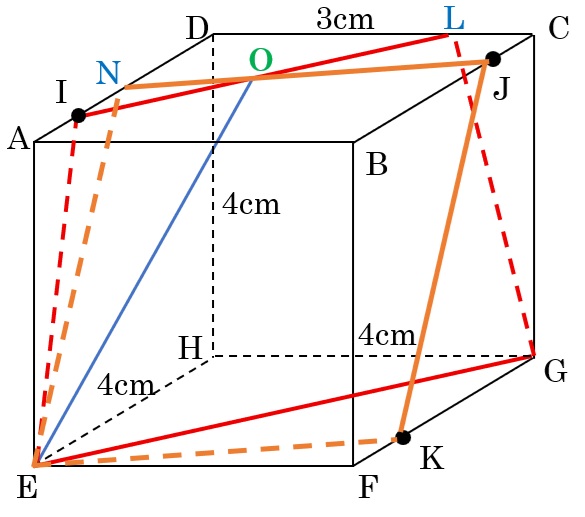
切り口の線ILとNJは点Oで交わっています。
また点Eでも交わっているので、EとOを結ぶ直線が、2面の交わる直線部分です。
このとき、点Bを含む方の立体の体積は、⑵で求めた立体から三角すいE-INOを引けば求められそうですね。
三角すいE-INOの底面は、真上からの図で考えると分かりやすそうです。

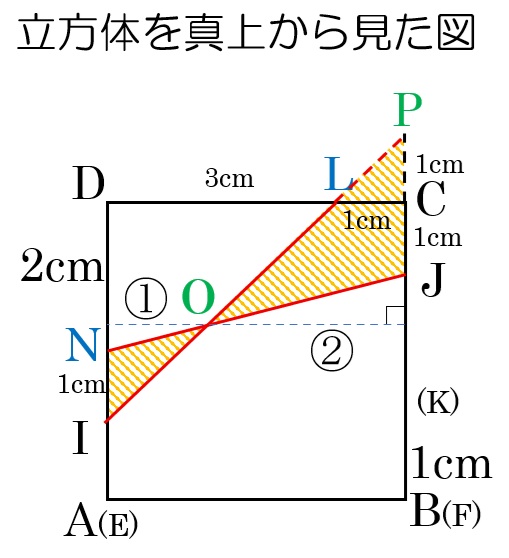
Pの部分を付け足すと、三角形INOと三角形PJOは相似で相似比は1：2より、図の①と②が決まる。
③＝4cmなので、①＝\(\frac{4}{3}\)cm
この三角すいE-INOの体積は、1×\(\frac{4}{3}\)÷2×4÷3＝\(\frac{8}{9}\)cm³
ですから、求めたい Bがふくまれる立体の体積は、24－\(\frac{8}{9}\)＝23\(\frac{1}{9}\)cm³

究学からのご案内

大阪星光を目指すなら

大阪星光を志望する人には、【中学受験算数ザ・バイブル「大阪星光学院」】をおすすめします。
過去問17年分のたぶんとても分かりやすくて丁寧な解説、過去17年分の過去問実物、過去17年分の入試問題を単元別に整理した問題集、問題傾向を突き詰めた単元別の問題集など。本気で合格を目指しているならぜひおすすめです。

➪2024年度大阪星光算数入試問題と解説、見本を無料進呈しています。