 入試問題解説
入試問題解説 東大寺2019年度算数 大問2
大問2は日暦算。出題頻度は高くないですが、きちんとやっておかないと後悔する、それが日暦算という問題です。ともかく、実際の問題を見てみましょう。西暦X年のカレンダーについて調べました。以下,○/△で○月△日を表すものとします。⑴ 西暦X年の2...
 入試問題解説
入試問題解説 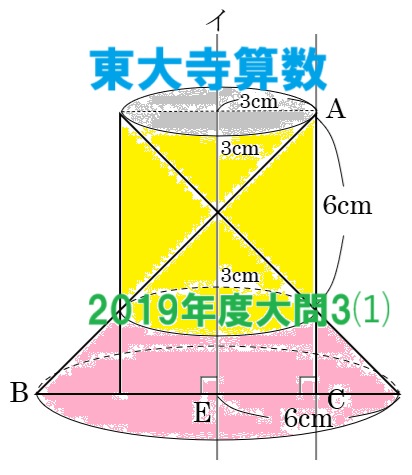 入試問題解説
入試問題解説 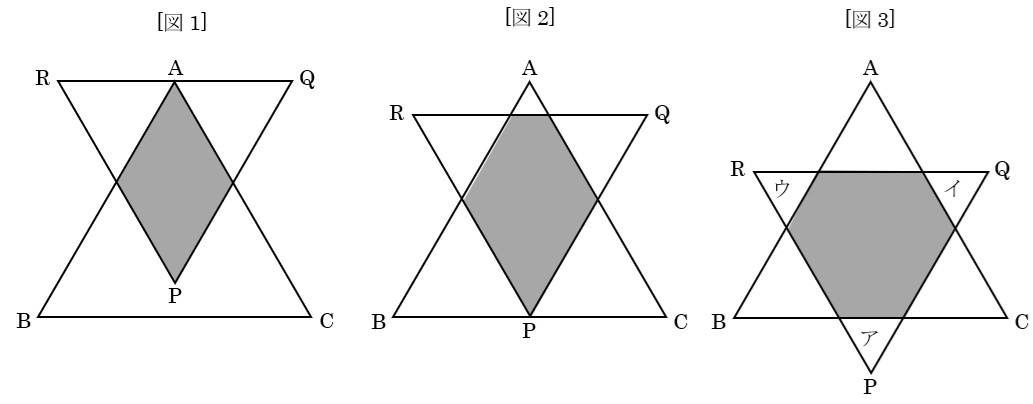 入試問題解説
入試問題解説  入試問題解説
入試問題解説  入試問題解説
入試問題解説  入試問題解説
入試問題解説  入試問題解説
入試問題解説  入試問題解説
入試問題解説  入試問題解説
入試問題解説  入試問題解説
入試問題解説